【题目】如图,在△ABC中,D、E分别是AB、AC的中点,过点E作EF∥AB,交BC于点F. 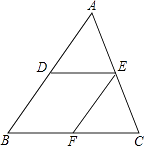
(1)求证:四边形DBFE是平行四边形;
(2)当△ABC满足什么条件时,四边形DBFE是菱形?为什么?
参考答案:
【答案】
(1)证明:∵D、E分别是AB、AC的中点,
∴DE是△ABC的中位线,
∴DE∥BC,
又∵EF∥AB,
∴四边形DBFE是平行四边形
(2)解:当AB=BC时,四边形DBFE是菱形.
理由如下:∵D是AB的中点,
∴BD= ![]() AB,
AB,
∵DE是△ABC的中位线,
∴DE= ![]() BC,
BC,
∵AB=BC,
∴BD=DE,
又∵四边形DBFE是平行四边形,
∴四边形DBFE是菱形
【解析】(1)根据三角形的中位线平行于第三边并且等于第三边的一半可得DE∥BC,然后根据两组对边分别平行的四边形是平行四边形证明;(2)根据邻边相等的平行四边形是菱形证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线y=2x与反比例函数y=
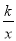 在第一象限内的图像交于点A(m,2),将直线y=2x向下平移后与反比例函数y=
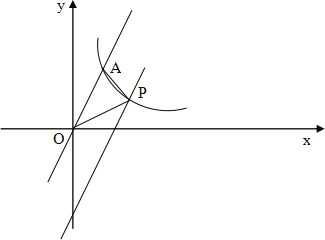
在第一象限内的图像交于点A(m,2),将直线y=2x向下平移后与反比例函数y=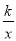 在第一象限内的图像交于点P,且△POA的面积为2.
在第一象限内的图像交于点P,且△POA的面积为2.(1)求k的值;
(2)求平移后的直线的函数解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数﹣4,﹣3,﹣2,﹣1,0,1,2,3,4中是方程x2+x﹣12=0的根有_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两直线AB,CD相交于点O,OE平分∠BOD,∠AOC∶∠AOD=7∶11.
(1)求∠COE的度数;
(2)若OF⊥OE,求∠COF的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A=-4a3-3+2a2+5a,B=3a3-a-a2,求:A-2B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列长度的各组线段能组成一个三角形的是( ).
A. 4cm,6cm,11cm B. 4cm,5cm,1cm
C. 3cm,4cm,5cm D. 2cm,3cm,6cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点A(1,﹣3),B(m,3)在同一反比例函数的图象上,则m的值为 .
相关试题

