Question

【题目】某厂家生产并销售某种产品，假设销售量与产量相等，如图中的折线ABD，线段CD分别表示该产品每千克生产成本y1（单位：元），销售价y2（单位：元）与产量x（单位：kg）之间的函数关系．

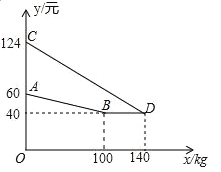
（1）请解释图中点D的实际意义．

（2）求线段CD所表示的y2与x之间的函数表达式．

（3）当该产品产量为多少时，获得的利润最大？最大利润是多少？

Answer 1

【答案】（1）点D的横坐标、纵坐标的实际意义：当产量为140kg时，该产品每千克生产成本与销售价相等，都为40元

（2）y2与x之间的函数表达式为y2=﹣x+124（0≤x≤140）

（3）当该产品的质量为80kg时，获得的利润最大，最大利润为2560元

【解析】

试题分析：（1）点D的横坐标、纵坐标的实际意义：当产量为140kg时，该产品每千克生产成本与销售价相等，都为40元；

（2）根据线段AB经过的两点的坐标利用待定系数法确定一次函数的表达式即可；

（3）先求出销售价y2与产量x之间的函数关系，利用：总利润=每千克利润×产量列出有关x的二次函数，求得最值即可．

试题解析：（1）点D的实际意义：当产量为140kg时，该产品每千克生产成本与销售价相等，都为40元．

（2）设线段CD所表示的y2与x之间的函数表达式为y2=k1x+b1，

∵点（0，124），（140，40）在函数y2=k1x+b1的图象上

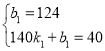∴，解得：，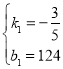

∴y2与x之间的函数表达式为y2=﹣x+124（0≤x≤140）；

（3）设线段AB所表示的y1与x之间的函数表达式为y1=k2x+b2，

∵点（0，60），（100，40）在函数y1=k2x+b2的图象上

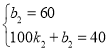∴，解得：，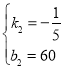

∴y1与x之间的函数表达式为y1=﹣x+60（0≤x≤100）

设产量为x千克时，获得的利润为W元

①当0≤x≤100时，W=[（﹣x+124）﹣（﹣x+60）]x=﹣（x﹣80）2+2560，

∴当x=80时，W的值最大，最大值为2560元．

②当100≤x≤140时，W=[（﹣x+124）﹣40]x=﹣（x﹣70）2+2940

由﹣＜0知，当x≥70时，W随x的增大而减小

∴当x=100时，W的值最大，最大值为2400元．

∵2560＞2400，

∴当该产品的质量为80kg时，获得的利润最大，最大利润为2560元．