【题目】如图,在△ABC中,AB=AC,∠A=40°,AB的垂直平分线交AB于点D,交AC于点E,连接BE,则∠CBE的度数为 . 
参考答案:
【答案】30°
【解析】∵AB=AC,∠A=40°,
∴∠ABC=∠C=70°,
∵DE是AB的垂直平分线,
∴EA=EB,
∴∠EBA=∠A=40°,
∴∠CBE=∠ABC﹣∠EBA=30°,
所以答案是:30°.
【考点精析】根据题目的已知条件,利用线段垂直平分线的性质和等腰三角形的性质的相关知识可以得到问题的答案,需要掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等;等腰三角形的两个底角相等(简称:等边对等角).
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题:
(1)(﹣8)+3+10+(﹣2)
(2)(﹣2)×(﹣6)÷(﹣
 )
)(3)(﹣1)100×2+(﹣2)3÷4
(4)2(a﹣3b)+3(2b﹣3a)
-
科目: 来源: 题型:
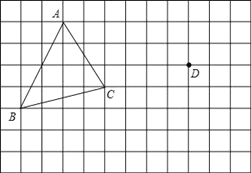
查看答案和解析>>【题目】在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示.现将△ABC平移,使点A变换为点D,点E、F分别是B、C的对应点.
(1)请画出平移后的△DEF.
(2)若连接AD、CF,则这两条线段之间的关系是 .
(3)画出△ABC的BC边上的高AM。
(4)满足三角形ACP的面积等于三角形ACB的面积的格点P有 个(不和B重合)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2﹣bx+0.5b﹣a与x轴交于A、B两点,则线段AB的最小值为( )
A.0.5
B.2
C.
D.无法确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,△ABC在直角坐标系内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2)(正方形网格中每个小正方形的边长均为一个单位长度).

①画出△ABC向下平移4个单位长度得到的△A1B1C1 , 点C1的坐标是 ;
②以点B为位似中心,在网格内画出△A2B2C2 , 使△A2B2C2与△ABC位似,且位似比为2:1 ,点C2的坐标是 ;
③若M(a,b)为线段AC上任一点,写出点M的对应点M2的坐标 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,﹣1).

①以O为位似中心在第二象限作位似比为1:2变换,得到对应的△A1B1C1 , 画出△A1B1C1 , 并写出C1的坐标;
②以原点O为旋转中心,画出把△ABC顺时针旋转90°的图形△A2B2C2 , 并写出C2的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).

(1)画出△ABC向下平移4个单位长度得到的△A1B1C1 ,
(2)点C1的坐标是;
(3)以点B为位似中心,在网格内画出△A2B2C2 ,
(4)使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 .
相关试题

