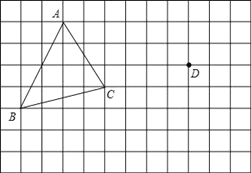
【题目】在正方形网格中，每个小正方形的边长均为1个单位长度，△ABC的三个顶点的位置如图所示．现将△ABC平移，使点A变换为点D，点E、F分别是B、C的对应点．

（1）请画出平移后的△DEF．

（2）若连接AD、CF，则这两条线段之间的关系是　　　　　　．

（3）画出△ABC的BC边上的高AM。

（4）满足三角形ACP的面积等于三角形ACB的面积的格点P有 个（不和B重合）

参考答案：

【答案】（1）详见解析；（2）平行且相等；（3）详见解析；（4）4.

【解析】

（1）根据网格结构找出点B、C平移后的对应点E、F的位置，然后与点D顺次连接即可；
（2）根据平移的性质，对应点的连线平行且相等；

（3）根据网格结构和三角形的高线的定义作出图形即可；

（4）过B作AC的平行线，过D作AC的平行线，即可得出格点P有4个．

（1） 如图：

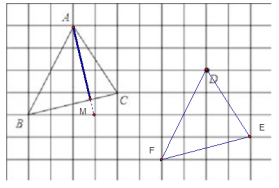
（2）根据平移的性质，对应点的连线平行且相等平行且相等；

（3）根据网格结构和三角形的高线的定义作出图形，如图：

（4）

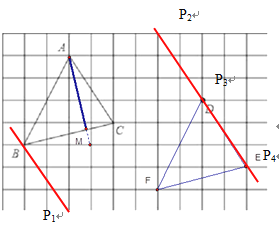
如图，过B作AC的平行线，过D作AC的平行线，
当点P在点P1，点P2，点P3，点P4处时，存在S△ACB=S△ACP，
∴格点P有4个．
故答案为：4．

关闭