【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①c<0,②abc>0,③a﹣b+c>0,④2a﹣3b=0,⑤c﹣4b>0.其中正确结论的个数有( )

A.1个 B.2个 C.3个 D.4个
参考答案:
【答案】D.
【解析】
试题分析:抛物线的开口向上,则a>0;
对称轴为x=![]() =
=![]() ,即3b=﹣2a,故b<0;
,即3b=﹣2a,故b<0;
抛物线交y轴于负半轴,则c<0;
①由以上c<0,正确;
②由a>0,b<0,c<0,得abc>0,正确;
③由图知:当x=﹣1时,y>0,则a﹣b+c>0,正确;
④由对称轴知:3b=﹣2a,即3b+2a=0,错误;
⑤由对称轴知:3b=﹣2a,即a=![]() b,函数解析式可写作y=
b,函数解析式可写作y=![]() bx2+bx+c;
bx2+bx+c;
由图知:当x=2时,y>0,即![]() b×4+2b+c>0,即c﹣4b>0,故⑤正确;
b×4+2b+c>0,即c﹣4b>0,故⑤正确;
∴正确的结论有四个:①②③⑤.
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一天早晨气温为-4℃,中午上升了7℃,半夜又下降了8℃,则半夜的气温是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列文字:我们知道对于一个图形,通过不同的方法计算图形的面积时,可以得到一个数学等式,例如由图a可以得到a2+3ab+2b2=(a+2b)(a+b).请回答下列问题:

(1)写出图b中所表示的数学等式是 .
(2)试画出一个长方形,使得用不同的方法计算它的面积时,能得到2a2+3ab+b2=(2a+b)(a+b).
(3)课本68页练一练,有一题:如图c,用四块完全相同的长方形拼成正方形,用不同的方法,计算图中阴影部分的面积,你能发现什么?(用含有x、y的多少表示) .
(4)通过上述的等量关系,我们可知:
当两个正数的和一定时,它们的差的绝对值越小则积越(填“大”或“小”).
当两个正数的积一定时,它们的差的绝对值越小则和越(填“大”或“小”).
(5)利用上面得出的结论,对于正数x,求:
①代数式:2x+ 的最小值是;
的最小值是;
②代数式:x(6﹣x)的最大值是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】将点P(﹣2,3)向右平移3个单位得到点P1 , 点P2与点P1关于原点对称,则P2的坐标是( )
A.(﹣5,﹣3)
B.(1,﹣3)
C.(﹣1,﹣3)
D.(5,﹣3) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
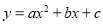 的图象经过点A(﹣2,0),点B(4,0),点D(2,4),与y轴交于点C,作直线BC,连接AC,CD.
的图象经过点A(﹣2,0),点B(4,0),点D(2,4),与y轴交于点C,作直线BC,连接AC,CD.(1)求抛物线的函数表达式;
(2)E是抛物线上的点,求满足∠ECD=∠ACO的点E的坐标;
(3)点M在y轴上且位于点C上方,点N在直线BC上,点P为第一象限内抛物线上一点,若以点C,M,N,P为顶点的四边形是菱形,求菱形的边长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,一牧童在A处牧马,牧童家在B处,A,B两处距河岸的距离AC,BD的长分别为700米,500米,且CD的距离为500米,天黑前牧童从A点将马牵到河边去饮水后,再赶回家,那么牧童最少要走( )米

A. 1100 B. 1200 C. 1300 D. 1400
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,为了测出旗杆AB的高度,在旗杆前的平地上选择一点C,测得旗杆顶部A的仰角为45°,在C、B之间选择一点D(C、D、B三点共线),测得旗杆顶部A的仰角为75°,且CD=8m.
(1)求点D到CA的距离;
(2)求旗杆AB的高.
(注:结果保留根号)

相关试题

