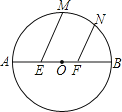
【题目】如图,已知⊙O的直径AB=6,E、F为AB的三等分点,M、N为![]() 上两点,且∠MEB=∠NFB=60°,则EM+FN= .
上两点,且∠MEB=∠NFB=60°,则EM+FN= .
参考答案:
【答案】![]()
【解析】
试题分析:延长ME交⊙O于G,根据圆的中心对称性可得FN=EG,过点O作OH⊥MG于H,连接MO,根据圆的直径求出OE,OM,再解直角三角形求出OH,然后利用勾股定理列式求出MH,再根据垂径定理可得MG=2MH,从而得解.
解:如图,延长ME交⊙O于G,
∵E、F为AB的三等分点,∠MEB=∠NFB=60°,
∴FN=EG,
过点O作OH⊥MG于H,连接MO,
∵⊙O的直径AB=6,
∴OE=OA﹣AE=![]() ×6﹣
×6﹣![]() ×6=3﹣2=1,
×6=3﹣2=1,
OM=![]() ×6=3,
×6=3,
∵∠MEB=60°,
∴OH=OEsin60°=1×![]() =
=![]() ,
,
在Rt△MOH中,MH=![]() =
=![]() =
=![]() ,
,
根据垂径定理,MG=2MH=2×![]() =
=![]() ,
,
即EM+FN=![]() .
.
故答案为:![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】山西特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20千克,若该专卖店销售这种核桃要想平均每天获利2240元,请回答:
(1)每千克核桃应降价多少元?
(2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y=ax2+bx+c的图象过A(2,0),B(0,﹣1)和C(4,5)三点.
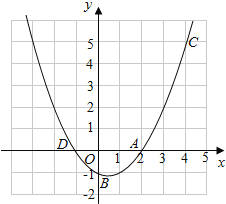
(1)求二次函数的解析式;
(2)设二次函数的图象与x轴的另一个交点为D,求点D的坐标;
(3)在同一坐标系中画出直线y=x+1,并写出当x在什么范围内时,一次函数的值大于二次函数的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某科技馆对学生参观实行优惠,个人票为每张6元,另有团体票可售,票价45元,每票最多限10人入馆参观.
(1)如果参观的学生人数36人,至少应付多少元?
(2)如果参观的学生人数为48人,至少应付多少元?
(3)如果参观的学生人数为一个两位数
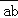 (a表示十位上的数字,b表示个位上的数字),用含a、b的代数式表示至少应付给科技馆的总金额.
(a表示十位上的数字,b表示个位上的数字),用含a、b的代数式表示至少应付给科技馆的总金额. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点O在线段AB上,点C、D分别是AO、BO的中点

(1)AO= CO;BO= DO;
(2)若CO=3cm,DO=2cm,求线段AB的长度;
(3)若线段AB=10,小明很轻松地求得CD=5.他在反思过程中突发奇想:若点O在线段AB的延长线上,原有的结论“CD=5”是否仍然成立呢?请帮小明画出图形分析,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形一定是轴对称图形的是( )
A.直角三角形 B.平行四边形 C.直角梯形 D.正方形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示:在平面直角坐标系中,以点M(0,
 )为圆心,2
)为圆心,2 为半径作⊙M交x轴于A,B两点,交y轴于C,D两点,连接AM并延长交⊙M于点P,连接PC交x轴于点E.
为半径作⊙M交x轴于A,B两点,交y轴于C,D两点,连接AM并延长交⊙M于点P,连接PC交x轴于点E.
(1)求点C,P的坐标;
(2)求弓形
 的面积;
的面积;(3)探求线段BE和OE存在何种数量关系,并证明你所得到的结论.
相关试题

