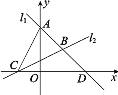
【题目】如图,直线l1过点A(0,4)与点D(4,0),直线l2:y=![]() x+1与x轴交于点C,两直线l1,l2相交于点B.
x+1与x轴交于点C,两直线l1,l2相交于点B.
(1)求直线l1的函数表达式;
(2)求点B的坐标;
(3)求△ABC的面积.
参考答案:
【答案】(1) y=-x+4;(2)点B的坐标为(2,2);(3)6.
【解析】
(1)利用待定系数法即可求出直线l1的函数关系式为y=-x+4;
(2)解方程组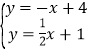 即可确定B点坐标;
即可确定B点坐标;
(3)求出点C坐标,根据S△ABC=S△ACD-S△BCD进行计算即可得.
(1)设直线l1的函数表达式为y=kx+b,
根据题意,得![]() ,解得:
,解得:![]() ,
,
所以直线l1的函数表达式为y=-x+4;
(2)根据题意,得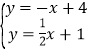 ,解得:
,解得:![]() ,
,
所以点B的坐标为(2,2);
(3)直线y=![]() x+1与x轴交于点C,所以点C坐标为(-2,0),
x+1与x轴交于点C,所以点C坐标为(-2,0),
所以CD=6,
所以,S△ABC=S△ACD-S△BCD=![]() =6.
=6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知一次函数y=﹣
 x+6与x,y轴分别交于A,B两点,点C(0,n)是y轴上一点,把坐标平面沿直线AC折叠,点B刚好落在x轴上,则点C的坐标是( )
x+6与x,y轴分别交于A,B两点,点C(0,n)是y轴上一点,把坐标平面沿直线AC折叠,点B刚好落在x轴上,则点C的坐标是( )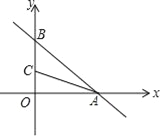
A. (0,3) B. (0,
 ) C. (0,
) C. (0, ) D. (0,
) D. (0, )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】为降低空气污染,公交公司决定全部更换节能环保的燃气公交车.计划购买A型和B型两种公交车共10辆,其中每台的价格,年均载客量如表:
A型
B型
价格(万元/辆)
a
b
年均载客量(万人/年/辆)
60
100
若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元
(1)求购买每辆A型公交车和每辆B型公交车分别多少万元?
(2)如果该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车年均载客总和不少于680万人次,有哪几种购车方案?请你设计一个方案,使得购车总费用最少. -
科目: 来源: 题型:
查看答案和解析>>【题目】“农民也可以报销医疗费了!”这是某市推行新型农村医疗合作的成果.村民只要每人每年交10元钱,就可以加入合作医疗,每年先由自己支付医疗费,年终时可得到按一定比例返回的返回款.这一举措极大地增强了农民抵御大病风险的能力.小华与同学随机调查了他们乡的一些农民,根据收集到的数据绘制了以下的统计图.

根据以上信息,解答以下问题:
(1)本次调查了多少村民,被调查的村民中,有多少人参加合作医疗得到了返回款;
(2)该乡若有10 000村民,请你估计有多少人参加了合作医疗?要使两年后参加合作医疗的人数增加到9 680人,假设这两年的年增长率相同,求这个年增长率. -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校计划组织全校1441名师生到相关部门规划的林区植树,经过研究,决定租用当地租车公司一共62辆
 两种型号客车作为交通工具.
两种型号客车作为交通工具.下表是租车公司提供给学校有关两种型号客车的载客量和租金信息:
型号
载客量
租金单价

30人/辆
380元/辆

20人/辆
280元/辆
注:载客量指的是每辆客车最多可载该校师生的人数.设学校租用
 型号客车
型号客车 辆,租车总费用为
辆,租车总费用为 元.
元.(1)求
 与
与 的函数解析式,请直接写出
的函数解析式,请直接写出 的取值范围;
的取值范围;(2)若要使租车总费用不超过21940元,一共有几种租车方案?哪种租车方案总费用最省?最省的总费用是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于有理数a、b,定义运算:a
 b=a×b-a-b+1.
b=a×b-a-b+1.(1)计算5
 (-2)与(-2)
(-2)与(-2) 5的值,并猜想a
5的值,并猜想a b与b
b与b a的大小关系;
a的大小关系;(2)求(-3)
 [4
[4 (-2)]的值.
(-2)]的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】从甲地到乙地,先是一段平路,然后是一段上坡路。小明骑车从甲地出发,到达乙地后立即原路返回甲地,途中休息了一段时间。假设小明骑车在平路、上坡、下坡时分别保持匀速前进.已知小明骑车上坡的速度比平路上的速度每小时少5km,下坡的速度比在平路上的速度每小时多5km。设小明出发xh后,到达离甲地y km的地方,图中的折线OABCDE表示y与x之间的函数关系.
(1)小明骑车在平路上的速度为 km/h;他途中休息了 h;
(2)求线段AB,BC所表示的y与
 之间的函数关系式;
之间的函数关系式;(3)如果小明两次经过途中某一地点的时间间隔为0.15h,那么该地点离甲地多远?

相关试题

