【题目】如图,已知抛物线y=ax2+c过点(﹣2,2),(4,5),过定点F(0,2)的直线l:y=kx+2与抛物线交于A、B两点,点B在点A的右侧,过点B作x轴的垂线,垂足为C.
(1)求抛物线的解析式;
(2)当点B在抛物线上运动时,判断线段BF与BC的数量关系(>、<、=),并证明你的判断;
(3)P为y轴上一点,以B、C、F、P为顶点的四边形是菱形,设点P(0,m),求自然数m的值;
(4)若k=1,在直线l下方的抛物线上是否存在点Q,使得△QBF的面积最大?若存在,求出点Q的坐标及△QBF的最大面积;若不存在,请说明理由.
参考答案:
【答案】
(1)
解:把点(﹣2,2),(4,5)代入y=ax2+c得 ![]() ,解得
,解得 ![]() ,
,
所以抛物线解析式为y= ![]() x2+1;
x2+1;
(2)
解:BF=BC.
理由如下:
设B(x, ![]() x2+1),而F(0,2),
x2+1),而F(0,2),
∴BF2=x2+( ![]() x2+1﹣2)2=x2+(
x2+1﹣2)2=x2+( ![]() x2﹣1)2=(
x2﹣1)2=( ![]() x2+1)2,
x2+1)2,
∴BF= ![]() x2+1,
x2+1,
∵BC⊥x轴,
∴BC= ![]() x2+1,
x2+1,
∴BF=BC;
(3)
解:如图1,
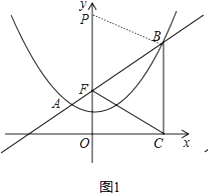
m为自然数,则点P在F点上方,
∵以B、C、F、P为顶点的四边形是菱形,
∴CB=CF=PF,
而CB=FB,
∴BC=CF=BF,
∴△BCF为等边三角形,
∴∠BCF=60°,
∴∠OCF=30°,
在Rt△OCF中,CF=2OF=4,
∴PF=CF=4,
∴P(0,6),
即自然数m的值为6;
(4)
解:作QE∥y轴交AB于E,如图2,
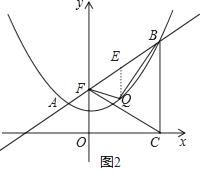
当k=1时,一次函数解析式为y=x+2,
解方程组 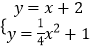 得
得 ![]() 或
或 ![]() ,则B(1+
,则B(1+ ![]() ,3+
,3+ ![]() ),
),
设Q(t, ![]() t2+1),则E(t,t+2),
t2+1),则E(t,t+2),
∴EQ=t+2﹣( ![]() t2+1)=﹣
t2+1)=﹣ ![]() t2+t+1,
t2+t+1,
∴S△QBF=S△EQF+S△EQB= ![]() (1+
(1+ ![]() )EQ=
)EQ= ![]() (1+
(1+ ![]() ))(﹣
))(﹣ ![]() t2+t+1)=﹣
t2+t+1)=﹣ ![]() (t﹣2)2+
(t﹣2)2+ ![]() +1,
+1,
当t=2时,S△QBF有最大值,最大值为 ![]() +1,此时Q点坐标为(2,2).
+1,此时Q点坐标为(2,2).
【解析】(1)利用待定系数法求抛物线解析式;(2)设B(x, ![]() x2+1),而F(0,2),利用两点间的距离公式得到BF2=x2+(
x2+1),而F(0,2),利用两点间的距离公式得到BF2=x2+( ![]() x2+1﹣2)2=,再利用配方法可得到BF=
x2+1﹣2)2=,再利用配方法可得到BF= ![]() x2+1,由于BC=
x2+1,由于BC= ![]() x2+1,所以BF=BC;(3)如图1,利用菱形的性质得到CB=CF=PF,加上CB=FB,则可判断△BCF为等边三角形,所以∠BCF=60°,则∠OCF=30°,于是可计算出CF=4,所以PF=CF=4,从而得到自然数m的值为6;(4)作QE∥y轴交AB于E,如图2,先解方程组
x2+1,所以BF=BC;(3)如图1,利用菱形的性质得到CB=CF=PF,加上CB=FB,则可判断△BCF为等边三角形,所以∠BCF=60°,则∠OCF=30°,于是可计算出CF=4,所以PF=CF=4,从而得到自然数m的值为6;(4)作QE∥y轴交AB于E,如图2,先解方程组 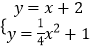 得B(1+
得B(1+ ![]() ,3+
,3+ ![]() ),设Q(t,
),设Q(t, ![]() t2+1),则E(t,t+2),则EQ=﹣
t2+1),则E(t,t+2),则EQ=﹣ ![]() t2+t+1,则S△QBF=S△EQF+S△EQB=
t2+t+1,则S△QBF=S△EQF+S△EQB= ![]() (1+
(1+ ![]() )EQ=
)EQ= ![]() (1+
(1+ ![]() ))(﹣
))(﹣ ![]() t2+t+1),然后根据二次函数的性质解决问题.
t2+t+1),然后根据二次函数的性质解决问题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB=90°,反比例函数y=﹣
 (x<0)的图象过点A(﹣1,a),反比例函数y=
(x<0)的图象过点A(﹣1,a),反比例函数y=  (k>0,x>0)的图象过点B,且AB∥x轴.
(k>0,x>0)的图象过点B,且AB∥x轴. 
(1)求a和k的值;
(2)过点B作MN∥OA,交x轴于点M,交y轴于点N,交双曲线y= 于另一点,求△OBC的面积.
于另一点,求△OBC的面积. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】为积极响应政府提出的“绿色发展低碳出行”号召,某社区决定购置一批共享单车.经市场调查得知,购买3辆男式单车与4辆女式单车费用相同,购买5辆男式单车与4辆女式单车共需16000元.
(1)求男式单车和女式单车的单价;
(2)该社区要求男式单比女式单车多4辆,两种单车至少需要22辆,购置两种单车的费用不超过50000元,该社区有几种购置方案?怎样购置才能使所需总费用最低,最低费用是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB、CD是⊙O的直径,BE是⊙O的弦,且BE∥CD,过点C的切线与EB的延长线交于点P,连接BC.

(1)求证:BC平分∠ABP;
(2)求证:PC2=PBPE;
(3)若BE﹣BP=PC=4,求⊙O的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列算式运算结果正确的是( )
A.(2x5)2=2x10
B.(﹣3)﹣2=
C.(a+1)2=a2+1
D.a﹣(a﹣b)=﹣b -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形的周长是10,底边长y是腰长x的函数,则下列图象中,能正确反映y与x之间函数关系的图象是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个几何体的主视图和俯视图如图所示,若这个几何体最多有a个小正方体组成,最少有b个小正方体组成,则a+b等于( )
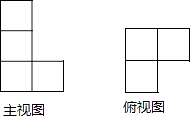
A.10
B.11
C.12
D.13
相关试题

