【题目】如图,已知:如图,在直角坐标系中,有菱形OABC,A点的坐标为(10,0),对角线OB、AC相交于D点,双曲线y= ![]() (x>0)经过D点,交BC的延长线于E点,且OBAC=160,有下列四个结论:
(x>0)经过D点,交BC的延长线于E点,且OBAC=160,有下列四个结论:
①双曲线的解析式为y= ![]() (x>0);②E点的坐标是(5,8);③sin∠COA=
(x>0);②E点的坐标是(5,8);③sin∠COA= ![]() ;④AC+OB=12
;④AC+OB=12 ![]() .其中正确的结论有( )
.其中正确的结论有( )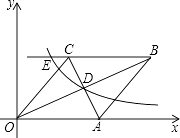
A.1个
B.2个
C.3个
D.4个
参考答案:
【答案】B
【解析】解:过点C作CF⊥x轴于点F,
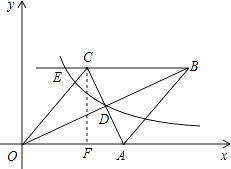
∵OBAC=160,A点的坐标为(10,0),
∴OACF= ![]() OBAC=
OBAC= ![]() ×160=80,菱形OABC的边长为10,
×160=80,菱形OABC的边长为10,
∴CF= ![]() =
= ![]() =8,
=8,
在Rt△OCF中,
∵OC=10,CF=8,
∴OF= ![]() =
= ![]() =6,
=6,
∴C(6,8),
∵点D时线段AC的中点,
∴D点坐标为( ![]() ,
, ![]() ),即(8,4),
),即(8,4),
∵双曲线y= ![]() (x>0)经过D点,
(x>0)经过D点,
∴4= ![]() ,即k=32,
,即k=32,
∴双曲线的解析式为:y= ![]() (x>0),故①错误;
(x>0),故①错误;
∵CF=8,
∴直线CB的解析式为y=8,
∴ 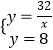 ,解得x=4,y=8,
,解得x=4,y=8,
∴E点坐标为(4,8),故②错误;
∵CF=8,OC=10,
∴sin∠COA= ![]() =
= ![]() =
= ![]() ,故③正确;
,故③正确;
∵A(10,0),C(6,8),
∴AC= ![]() =4
=4 ![]() ,
,
∵OBAC=160,
∴OB= ![]() =
= ![]() =8
=8 ![]() ,
,
∴AC+OB=4 ![]() +8
+8 ![]() =12
=12 ![]() ,故④正确.
,故④正确.
所以答案是:B.
【考点精析】本题主要考查了勾股定理的概念和菱形的性质的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,分别以直角三角形三边为边向外作等边三角形,面积分别为S1、S2、S3;如图2,分别以直角三角形三个顶点为圆心,三边长为半径向外作圆心角相等的扇形,面积分别为S4、S5、S6 . 其中S1=16,S2=45,S5=11,S6=14,则S3+S4=( )

A.86
B.64
C.54
D.48 -
科目: 来源: 题型:
查看答案和解析>>【题目】抗震救灾中,某县粮食局为了保证库存粮食的安全,决定将甲、乙两个仓库的粮食,全部转移到具有较强抗震功能的A、B两仓库.已知甲库有粮食100吨,乙库有粮食80吨,而A库的容量为70吨,B库的容量为110吨.从甲、乙两库到A、B两库的路程和运费如下表:(表中“元/吨千米”表示每吨粮食运送1千米所需人民币)
路程(千米)
运费(元/吨千米)
甲库
乙库
甲库
乙库
A库
20
15
12
12
B库
25
20
10
8
(1)若甲库运往A库粮食x吨,请写出将粮食运往A、B两库的总运费y(元)与x(吨)的函数关系式;
(2)当甲、乙两库各运往A、B两库多少吨粮食时,总运费最省,最省的总运费是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长均为1个单位的正方形网格图中,建立了平面直角坐标系xOy,按要求解答下列问题:

(1)写出△ABC三个顶点的坐标;
(2)画出△ABC向右平移6个单位后得到的图形△A1B1C1;
(3)求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O是Rt△ABC的外接圆,∠ACB=90°,∠A=25°,过点C作圆O的切线,交AB的延长线于点D,则∠D的度数是 .
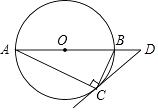
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一张等边三角形纸片沿中位线剪成4个小三角形,称为第一次操作:然后,将其中的一个三角形按同样方式再剪成4个小三角形,共得到7个小三角形,称为第二次操作;再将其中一个三角形按同样方式再剪成4个小三角形,共得到10个小三角形,称为第三次操作;…根据以上操作,①第七次操作共得到个三角形;②若要得到220个小三角形,则需要操作的次数是 .
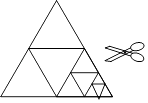
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)计算:(﹣ )﹣2﹣|
)﹣2﹣| 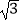 ﹣1|+(﹣
﹣1|+(﹣ 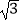 +1)0+3tan30°
+1)0+3tan30°
(2)解方程: +
+ 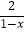 =4.
=4.
相关试题

