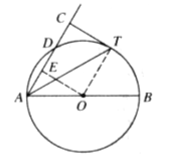
【题目】如图,AB是⊙O直径,D为⊙O上一点,AT 平分∠BAD交⊙O于点 T,过 T 作AD的垂线交 A D的延长线于点 C。
(1)求证:CT为⊙O的切线;
(2)若⊙O半径为2,CT=![]() ,求AD的长。
,求AD的长。

参考答案:
【答案】(1)证明见解析(2)2
【解析】
试题分析:(1)连接OT,根据角平分线的性质,以及直角三角形的两个锐角互余,证得CT⊥OT,CT为⊙O的切线;
(2)证明四边形OTCE为矩形,求得OE的长,在直角△OAE中,利用勾股定理即可求解.
试题解析:(1)连接OT
∵OA=OT,∴∠OAT=∠OTA
又∵AT 平分∠BAD,∴∠DAT=∠OAT
∴∠DAT=∠OTA,∴OT∥AC
又∵CT⊥AC,∴CT⊥OT
∴CT为⊙O的切线
(2)过O作OE⊥AD于E,则 E为AD中点
又∵CT⊥AC,∴OE∥CT
∴四边形 OTCE 为矩形
∵CT=![]() ,∴OE=
,∴OE=![]()
又∵OA=2
∴在 Rt△OAE 中,AE=![]()
∴AD=2AE=2
-
科目: 来源: 题型:
查看答案和解析>>【题目】把2(a-3)+a(3-a)提取公因式(a-3)后,另一个因式为( )
A. a-2 B. a+2 C. 2-a D. -2-a
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(-1)2+20-|-3|的值等于( )
A. -1 B. 0 C. 1 D. 5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,已知正比例函数
 与一次函数
与一次函数 的图像交于点A.
的图像交于点A.(1)求点A的坐标;
(2)设x轴上一点P(a,b),过点P作x轴的垂线(垂线位于点A的右侧),分别交
 和
和 的图像于点B、C,连接OC,若BC=
的图像于点B、C,连接OC,若BC= OA,求△OBC的面积.
OA,求△OBC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程x2+3x+1=0的根的情况是: .
-
科目: 来源: 题型:
查看答案和解析>>【题目】(6 分)为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段达到节水的目的,该市自来水收费的收费标准如下表:
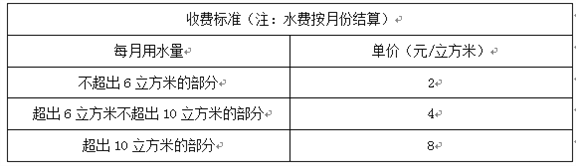
例如:某户居民1月份用水8立方米,应收水费为2×6+4×(8-6)=20(元).
请根据上表的内容解答下列问题:
⑴若某户居民2月份用水5立方米,则应收水费________元;
⑵若某户居民3月份交水费36元,则用水量为________立方米;
⑶若某户居民4月份用水a立方米(其中6<a<10),请用含a的代数式表示应收水费________元.
⑷若某户居民 5、6 两个月共用水18立方米(6月份用水量超过了10立方米),设5月份用水x立方米,请用含x的代数式表示该居民5、6两个月共交水费多少元?
-
科目: 来源: 题型:
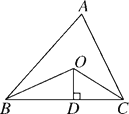
查看答案和解析>>【题目】如图,在△ABC中,点O是∠ABC、∠ACB平分线的交点,AB+BC+AC=20,过O作OD⊥BC于D点,且OD=3,求△ABC的面积.
相关试题

