【题目】如图1,在四边形ABCD的边AB上任取一点E(点E不与点A、点B重合),分别连接ED,EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的相似点;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的强相似点.解决问题:
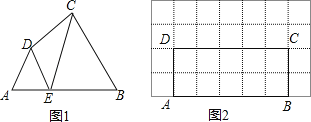
(1)如图1,∠A=∠B=∠DEC=55°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;
(2)如图2,在矩形ABCD中,AB=5,BC=2,且A,B,C,D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图2中画出矩形ABCD的边AB上的一个强相似点E.
参考答案:
【答案】(1)点E是四边形ABCD的边AB上的相似点.理由见解析;(2)画图见解析.
【解析】
试题分析:(1)要证明点E是四边形ABCD的AB边上的相似点,只要证明有一组三角形相似就行,很容易证明△ADE∽△BEC,所以问题得解.
(2)根据两个直角三角形相似得到强相似点的两种情况即可(以CD为直径画弧,取该弧与AB的一个交点即为所求).
解:(1)点E是四边形ABCD的边AB上的相似点.
理由:∵∠A=55°,
∴∠ADE+∠DEA=125°.
∵∠DEC=55°,
∴∠BEC+∠DEA=125°.
∴∠ADE=∠BEC.
∵∠A=∠B,
∴△ADE∽△BEC.
∴点E是四边形ABCD的AB边上的相似点.
(2)作图如下:
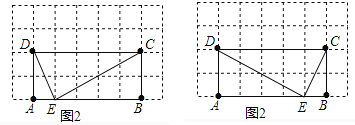
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式a3-4a=______________
-
科目: 来源: 题型:
查看答案和解析>>【题目】中国科学家屠呦呦获得了诺贝尔生理学或医学奖,她研发的抗疟新药每年能为近120万婴幼儿免除疟疾的危害.其中120万用科学记数法表示为( )
A.12×103
B.1.2×104
C.1.2×106
D.1.2×108 -
科目: 来源: 题型:
查看答案和解析>>【题目】 我们已经学习了利用配方法解一元二次方程,其实配方法还有其它重要应用.
例:已知x可取任何实数,试求二次三项式2x2-12x+14的值的范围.
解:2x2-12x+14=2(x2-6x)+14=2(x2-6x+32-32)+14
=2[(x-3)2-9]+14=2(x-3)2-18+14=2(x-3)2-4.
∵无论x取何实数,总有(x-3)2≥0,∴2(x-3)2-4≥-4.
即无论x取何实数,2x2-12x+14的值总是不小于-4的实数.
问题:已知x可取任何实数,则二次三项式-3x2+12x-11的最值情况是( )
A.有最大值-1 B.有最小值-1 C.有最大值1 D.有最小值1
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个正方形和两个等边三角形的位置如图所示,若∠3=50°,则∠1+∠2=( )
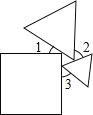
A.90° B.100° C.130° D.180°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,AC与BD交于点O,点E,F都在BD上,BE=DF.
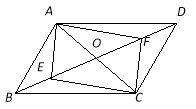
(1)求证:四边形AECF是平行四边形.
(2)若AB⊥AC,AB=4,AC=6,当□AECF是矩形时,求BE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB∥CD,∠BCD=90°,AB=AD=10cm,BC=8cm.点P从点A出发,以3cm/s的速度沿折线ABCD方向运动,点Q从点D出发,以2cm/s的速度沿线段DC向点C运动.已知P,Q两点同时出发,当点Q到达点C时,P,Q停止运动,设运动时间为t(s).

(1)、求CD的长.
(2)、当四边形PBQD为平行四边形时,求四边形PBQD的周长.
(3)、当点P在折线BCD上运动时,是否存在某一时刻,使得△BPQ的面积为16cm2?若存在,请求出满足条件的t的值;若不存在,请说明理由.
相关试题

