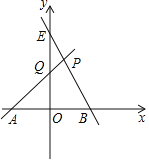
【题目】如图,已知直线AQ与x轴负半轴交于点A,与y轴正半轴交于点Q,∠QAO=45°,直线AQ在y轴上的截距为2,直线BE:y=-2x+8与直线AQ交于点P.
(1)求直线AQ的解析式;
(2)在y轴正半轴上取一点F,当四边形BPFO是梯形时,求点F的坐标.
(3)若点C在y轴负半轴上,点M在直线PA上,点N在直线PB上,是否存在以Q、C、M、N为顶点的四边形是菱形,若存在请求出点C的坐标;若不存在请说明理由.
参考答案:
【答案】(1)直线AQ的解析式为y=x+2;(2)F(0,4);(3)存在,C(0,![]() )或C(0,-10)
)或C(0,-10)
【解析】
(1)利用待定系数法即可求出直线AQ的解析式;
(2)先求出直线AQ和直线BE的交点P的坐标,由PF∥x轴可知F横坐标为0,纵坐标与点P的纵坐标相等;
(3)分CQ为菱形的对角线与CQ是菱形的一条边两种情况讨论.
解:(1)设直线AQ的解析式为y=kx+b,
∵直线AQ在y轴上的截距为2,
∴b=2,
∴直线AQ的解析式为y=kx+2,
∴OQ=2,
在Rt△AOQ中,∠OAQ=45°,
∴OA=OQ=2,
∴A(-2,0),
∴-2k+2=0,
∴k=1,
∴直线AQ的解析式为y=x+2;
(2)由(1)知,直线AQ的解析式为y=x+2①,
∵直线BE:y=-2x+8②,
联立①②解得![]() ,
,
∴P(2,4),
∵四边形BPFO是梯形,
∴PF∥x轴,
∴F(0,4);
(3)设C(0,c),
∵以Q、C、M、N为顶点的四边形是菱形,
①当CQ是对角线时,CQ与MN互相垂直平分,
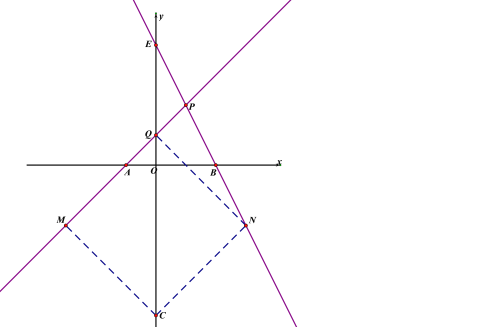
设C(0,c),
∵CQ的中点坐标为(0,![]() ),
),
∴点M,N的纵坐标都是![]() ,
,
∴M(![]() ,
,![]() ),N(
),N(![]() ,
,![]() ),
),
∴![]() +
+![]() =0,
=0,
∴c=-10,
∴C(0,-10),
②当CQ为边时,CQ∥MN,CQ=MN=QM,
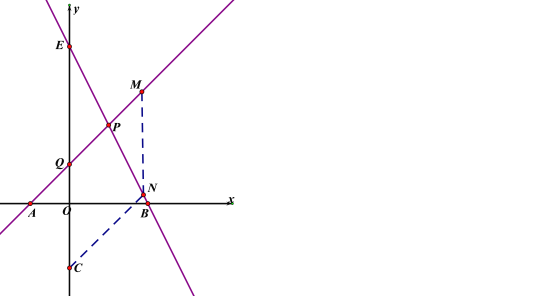
设M(m,m+2),
∴N(m,-2m+8),
∴|3m-6|=2-c=![]() |m|,
|m|,
∴m=![]() 或m=
或m=![]() ,
,
∴c=![]() 或c=
或c=![]() (舍),
(舍),
∴![]() ,
,
∴(0,![]() )或C(0,-10).
)或C(0,-10).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市居民用水实行阶梯水价,实施细则如下表:
分档水量
年用水量 (立方米)
水价 (元/立方米)
第一阶梯
0~180(含)
5.00
第二阶梯
181~260(含)
7.00
第三阶梯
260以上
9.00
例如,某户家庭年使用自来水200 m3,应缴纳:180×5+(200-180)×7=1040元;
某户家庭年使用自来水300 m3,应缴纳:180×5+(260-180)×7+(300-260)×9=1820元.
(1)小刚家2017年共使用自来水170 m3,应缴纳 元;小刚家2018年共使用自来水260 m3,应缴纳 元.
(2)小强家2018年使用自来水共缴纳1180元,他家2018年共使用了多少自来水?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在梯形
 ,
, ,过点
,过点 ,垂足为
,垂足为 ,并延长
,并延长 ,使
,使 ,联结
,联结 .
.(1)求证:四边形
 是平行四边形。
是平行四边形。(2)联结
 ,如果
,如果

-
科目: 来源: 题型:
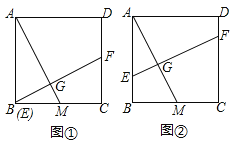
查看答案和解析>>【题目】如图,正方形ABCD,AB=4,点M是边BC的中点,点E是边AB上的一个动点,作EG⊥AM交AM于点G,EG的延长线交线段CD于点F.
(1)如图①,当点E与点B重合时,求证:BM=CF;
(2)设BE=x,梯形AEFD的面积为y,求y与x的函数解析式,并写出定义域.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明去离家2.4 km的体育馆看球赛,进场时,发现门票还放在家中,此时离比赛还有45 min,于是他立即步行(匀速)回家取票,在家取票用时2 min,取到票后,他马上骑自行车(匀速)赶往体育馆.已知小明骑自行车从家赶往体育馆比从体育馆步行回家所用时间少20 min,骑自行车的速度是步行速度的3倍.
(1)小明步行的速度是多少?
(2)小明能否在球赛开始前赶到体育馆?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,E、F是四边形ABCD的对角线AC上的两点,AF=CE,DF=BE,DF∥BE.

求证:(1)△AFD≌△CEB.(2)四边形ABCD是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上点A表示的数a、点B表示数b,a、b满足|a﹣30|+(b+6)2=0.点O是数轴原点.

(1)点A表示的数为 ,点B表示的数为 ,线段AB的长为 .
(2)若点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC,请在数轴上找一点C,使AC=2BC,则点C在数轴上表示的数为 .
(3)现有动点P、Q都从B点出发,点P以每秒1个单位长度的速度向终点A移动;当点P移动到O点时,点Q才从B点出发,并以每秒3个单位长度的速度向右移动,且当点P到达A点时,点Q就停止移动,设点P移动的时间为t秒,问:当t为多少时,P、Q两点相距4个单位长度?
相关试题

