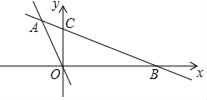
【题目】如图,在平面直角坐标系中,直线AB分别与x轴、y轴交于点B、C,与直线OA交于点A.已知点A的坐标为(﹣3,5),OC=4.
(1)分别求出直线AB、AO的解析式;
(2)求△ABO的面积.
参考答案:
【答案】(1)直线AB的解析式为y=﹣![]() x+4,直线AO的解析式为y
x+4,直线AO的解析式为y![]() x;(2)30.
x;(2)30.
【解析】
(1)由点A的坐标,利用待定系数法可求出直线AO的解析式,由OC及点C的位置可得出点C的坐标,结合点A的坐标,利用待定系数法即可求出直线AB的解析式;
(2)利用一次函数图象上点的坐标特征可求出OB的长度,过点A作AD⊥x轴于点D,由点A的坐标可得出AD的长度,再利用三角形的面积公式即可求出△ABO的面积.
设直线AO的解析式为y=kx(k≠0),
将A(﹣3,5)代入y=kx,得:5=﹣3k,解得:k![]() ,
,
∴直线AO的解析式为y![]() x.
x.
∵OC=4,点C在y轴正半轴,
∴点C的坐标为(0,4).
设直线AB的解析式为y=mx+n(m≠0),
将A(﹣3,5),C(0,4)代入y=mx+n,得:![]() ,
,
解得: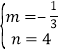 ,
,
∴直线AB的解析式为y![]() x+4.
x+4.
当y=0时,![]() x+4=0,解得:x=12,
x+4=0,解得:x=12,
∴OB=12.
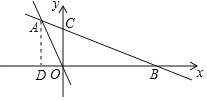
过点A作AD⊥x轴于点D,如图所示.
∵点A的坐标为(﹣3,5),
∴AD=5,
∴S△AOB![]() OBAD
OBAD![]() 12×5=30.
12×5=30.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=﹣x+m和y=2x+n的图象都经过A(﹣4,0),且与y轴分别交于B、C两点,则△ABC的面积为( )
A.48B.36C.24D.18
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,AC=BC,点G为AC中点,连结BG,CE⊥BG于F,交AB于E,连接GE,点H为AB中点,连接FH.以下结论:(1)∠ACE=∠ABG;(2)∠AGE=∠CGB:(3)若AB=10
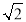 ,则BF=4
,则BF=4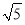 ;(4)FH平分∠BFE;(5)S△BGC=3S△CGE.其中正确结论的个数是( )
;(4)FH平分∠BFE;(5)S△BGC=3S△CGE.其中正确结论的个数是( )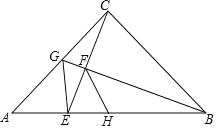
A.1B.2C.3D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△AOB的边OB在x轴上,AC⊥x轴于C,D为AC上一点,将△CBD沿BD翻折,使点C落在AB边上的E点.已知∠AOB=60°,AO=4
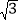 ,点B的坐标为(8+2
,点B的坐标为(8+2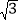 ,0),则点D的坐标为_____.
,0),则点D的坐标为_____.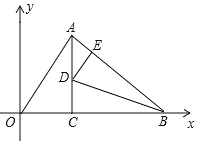
-
科目: 来源: 题型:
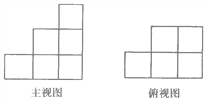
查看答案和解析>>【题目】由一些大小相同的小正方体组成的简单几何体的主视图和俯视图如图29-29所示.
(1)请你画出这个几何体的一种左视图.
(2)若组成这个几何体的小正方体的块数为n,请你写出n的所有可能值.
-
科目: 来源: 题型:
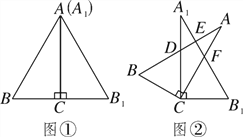
查看答案和解析>>【题目】将两块相同的含30°角的直角三角板按图①的方式放置,已知∠BAC=∠B1A1C=30°,AB=2BC.固定三角板A1B1C,然后将三角板ABC绕点C顺时针方向旋转至图②的位置,AB与A1C、A1B1分别交于点D、E,AC与A1B1交于点F.
(1)当旋转角等于20°时,∠BCB1=________度;
(2)当旋转角等于多少度时,AB与A1B1垂直?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,同时将点A(﹣1,0)、B(3,0)向上平移2个单位长度再向右平移1个单位长度,分别得到A、B的对应点C、D.连接AC,BD

(1)求点C、D的坐标,并描出A、B、C、D点,求四边形ABDC面积;
(2)在坐标轴上是否存在点P,连接PA、PC使S△PAC=S四边形ABCD?若存在,求点P坐标;若不存在,请说明理由.
相关试题

