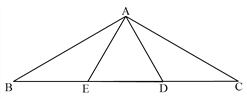
【题目】如果两个三角形的两条边对应相等,夹角互补,那么这两个三角形叫做互补三角形,如图2,分别以△ABC的边AB、AC为边向外作正方形ABDE和ACGF,则图中的两个三角形就是互补三角形.
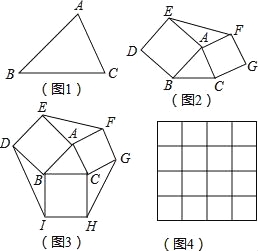
(1)用尺规将图1中的△ABC分割成两个互补三角形;
(2)证明图2中的△ABC分割成两个互补三角形;
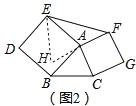
(3)如图3,在图2的基础上再以BC为边向外作正方形BCHI.
①已知三个正方形面积分别是17、13、10,在如图4的网格中(网格中每个小正方形的边长为1)画出边长为![]() 、
、![]() 、
、![]() 的三角形,并计算图3中六边形DEFGHI的面积.
的三角形,并计算图3中六边形DEFGHI的面积.
②若△ABC的面积为2,求以EF、DI、HG的长为边的三角形面积.
参考答案:
【答案】(1)作图见解析(2)证明见解析(3)①62;②6
【解析】
试题分析:(1)作BC边上的中线AD即可.
(2)根据互补三角形的定义证明即可.
(3)①画出图形后,利用割补法求面积即可.
②平移△CHG到AMF,连接EM,IM,则AM=CH=BI,只要证明S△EFM=3S△ABC即可.
试题解析:(1)如图1中,作BC边上的中线AD,△ABD和△ADC是互补三角形.
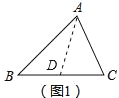
(2)如图2中,延长FA到点H,使得AH=AF,连接EH.
∵四边形ABDE,四边形ACGF是正方形,
∴AB=AE,AF=AC,∠BAE=∠CAF=90°,
∴∠EAF+∠BAC=180°,
∴△AEF和△ABC是两个互补三角形.
∵∠EAH+∠HAB=∠BAC+∠HAB=90°,
∴∠EAH=∠BAC,
∵AF=AC,
∴AH=AB,
在△AEH和△ABC中,
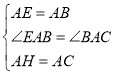
∴△AEH≌△ABC,
∴S△AEF=S△AEH=S△ABC.
(3)①边长为![]() 、
、![]() 、
、![]() 的三角形如图4所示.
的三角形如图4所示.
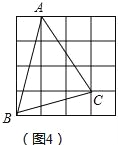
∵S△ABC=3×4﹣2﹣1.5﹣3=5.5,
∴S六边形=17+13+10+4×5.5=62.
②如图3中,平移△CHG到AMF,连接EM,IM,则AM=CH=BI,设∠ABC=x,
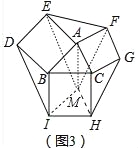
∵AM∥CH,CH⊥BC,
∴AM⊥BC,
∴∠EAM=90°+90°﹣x=180°﹣x,
∵∠DBI=360°﹣90°﹣90°﹣x=180°﹣x,
∴∠EAM=∠DBI,∵AE=BD,
∴△AEM≌△DBI,
∵在△DBI和△ABC中,DB=AB,BI=BC,∠DBI+∠ABC=180°,
∴△DBI和△ABC是互补三角形,
∴S△AEM=S△AEF=S△AFM=2,
∴S△EFM=3S△ABC=6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校在经典诵读活动中,对全校学生用A,B,C,D四个等级进行评价,现从中随机抽取若干个学生进行调查,绘制出了两幅不完整的统计图,如图所示,请你根据图中信息解答下列问题:

(1)共抽取了多少个学生进行调查?
(2)分别求出B等级的人数和图乙中B等级所占圆心角的度数.
(3)将图甲中的折线统计图补充完整. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB=AC,∠BAC=120°,AD⊥AB,AE⊥AC.
(1)求证:△ABE≌△ACD;
(2)求证:△ADE是等边三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】面对突如其来的疫情,全国广大医务工作者以白衣为战袍,义无反顾的冲在抗疫战争的一线,用生命捍卫人民的安全.据统计,全国共有346支医疗队,将近42600名医护工作者加入到支援湖北武汉的抗疫队伍,将42600用科学记数法表示为( )
A.0.426×105B.4.26×104C.42.6×103D.426×102
-
科目: 来源: 题型:
查看答案和解析>>【题目】用一副三角板的内角(其中一个三角板的内角是45°,45°,90°,另一个是30°,60°,90°)可以画出大于0°且小于180°的不同度数的角共有( )
A. 8种 B. 9种 C. 10种 D. 11种
-
科目: 来源: 题型:
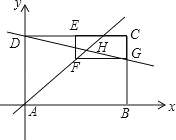
查看答案和解析>>【题目】如图,在矩形ABCD中,点A为坐标原点,点B在x轴正半轴,点D在y轴正半轴,点C坐标为(6,m),点E是CD的中点,以CE为一边在矩形ABCD的内部作矩形CEFG,使点F在直线y=x上,交线段BC于点G,直线DG的函数表达式为y=-
 x+4,直线DG和AF交于点H.
x+4,直线DG和AF交于点H.(1)求m的值;
(2)求点H的坐标;
(3)判断直线BE是否经过点H,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题.
(1)已知一个多边形的内角和是1260°,求这个多边形的边数.
(2)用一条长为18cm的细绳围成一个等腰三角形,若有一边长等于4cm,求另外两边长.
相关试题

