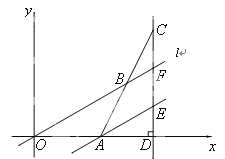
【题目】如图,在平面直角坐标系中,点A的坐标为(3,0),直线l与x轴正半轴夹角为30°,点B为直线l上的一个动点,延长AB至点C,使得AB=BC,过点C作CD⊥x轴于点D,交直线l于点F,过点A作AE∥l交直线CD于点E.
(1)、若点B的横坐标为6,则点C的坐标为(______,_____),DE的长为 ;
(2)、若点B的横坐标大于3,则线段CF的长度是否发生改变?若不变,请求出线段CF的长度;若改变,请说明理由;
(3)、连结BE,在点B的运动过程中,以OB为直径的⊙P与△ABE某一边所在的直线相切,请求出所有满足条件的DE的长.
参考答案:
【答案】(1)、C(9,![]() );DE=
);DE=![]() ;(2)、证明过程见解析;(3)、DE的长为
;(2)、证明过程见解析;(3)、DE的长为![]() 或
或![]() 或
或![]()
【解析】
试题分析:(1)、根据题意求出点C的坐标及DE的长度;(2)、过点A作AM⊥x轴于M,根据tan∠BOA的值求出AM的长度,然后证明△ABM和△CBF全等,从而得出CG=AM;(3)、本题需要分三种情况进行分类计算,首先分别画出图形,然后分别进行计算.
试题解析:(1)、C(9,![]() ) , DE=
) , DE=![]() ;
;
(2)、如图(1),过点A作AM⊥x轴于M ,∴∠OAM=90°, ∠BOA=30°, ∴AM=OAtan∠BOA=![]() .
.
∵B为AC的中点, ∴AB=BC 又∵AM∥CF, ∴∠AMB=∠CFB ,∠MAB=∠FCB,
∴△ABM≌△CBF ∴CF=AM=![]() . ∴线段CF的长度保持不变.
. ∴线段CF的长度保持不变.
(3)、如图1,过点B作BG⊥x轴于点G.易证, OB=2BG ,CD=2BG,
∴OB=CD.
(I)当点D在点A的右侧时,⊙P只能与BE相切,如图2.
设DE=![]() , 则OB=CD=
, 则OB=CD=![]() . ∵⊙P与BE相切于点B,
. ∵⊙P与BE相切于点B,
∴OB⊥BE. 易得BF=![]() EF=
EF=![]() .
.
∴OF=OB+BF=![]() . ∴OF=2DF, ∴
. ∴OF=2DF, ∴![]() =
=![]() .
.
解得![]() . ∴ DE=
. ∴ DE=![]() .
.
(II)当点D在线段OA上时,①若⊙P与直线AE相切,如图3,
易得,直线l与AE的距离是![]() . ∴ OB=3. ∴ CD=3. ∴DE=2CF-CD=
. ∴ OB=3. ∴ CD=3. ∴DE=2CF-CD=![]() .
.
②当⊙P与AB相切,如图4. ∴∠OBA=90°. ∴OB=OAtan∠OBA=![]() . ∴CD=
. ∴CD=![]() .
.
∴ DE=2CF-CD=![]() =
=![]() .
.
(III)当点D在点O的左侧时,⊙P只能与直线AE相切,如图5 ∵ 直线l与AE的距离是![]() ,
,
∴ OB=3.∴ CD=3. ∴ DE=2CF+CD=![]() .
.
综上所述,DE的长为![]() 或
或![]() 或
或![]() .
.





-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:点 A、C、B、D在同一条直线,∠M=∠N,AM=CN.请你添加一个条件,使△ABM≌△CDN,并给出证明.
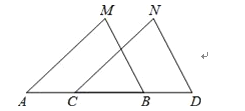
(1)你添加的条件是: ;
(2)证明:
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a>b,则下列式子中错误的是( )
A.a+2>b+2B.4a>4bC.﹣a>﹣bD.4a﹣3>4b﹣3
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P在第四象限,且到x轴的距离为4,到y轴的距离是2,则点P的坐标为( )
A. (4,﹣2) B. (﹣4,2) C. (﹣2,4) D. (2,﹣4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】点(x1,y1)、(x2,y2)在直线y=﹣x+b上,若x1<x2,则y1与y2大小关系是( )
A. y1<y2 B. y1=y2 C. y1>y2 D. 无法确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题是真命题的是( )
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.对角线互相垂直的平行四边形是矩形
C.四条边相等的四边形是菱形
D.正方形是轴对称图形,但不是中心对称图形
-
科目: 来源: 题型:
查看答案和解析>>【题目】某牧场,放养的鸵鸟和奶牛一共70只,已知鸵鸟和奶牛的腿数之和为196条,则鸵鸟的头数比奶牛多( )
A.20只
B.14只
C.15只
D.13只
相关试题

