搜索
【题目】如图，小明坐在堤边A处垂钓，河堤AC与水平面的夹角为30°，AC的长为
米，钓竿AO与水平线的夹角为60°，其长为3米，若AO与钓鱼线OB的夹角为60°，求浮漂B与河堤下端C之间的距离．
参考答案：
【答案】浮漂B与河堤下端C之间的距离为1.5米
【解析】试题分析：延长OA交BC于点D．先由倾斜角定义及三角形内角和定理求出
在Rt△ACD中, 
米，CD=2AD=3米，再证明△BOD是等边三角形，得到
米，然后根据BC=BDCD即可求出浮漂B与河堤下端C之间的距离．
试题解析：延长OA交BC于点D.
∵AO的倾斜角是
，
∴
∵
在Rt△ACD中, 
(米)，
∴CD=2AD=3米，
又
∴△BOD是等边三角形，
∴
(米)，
∴BC=BDCD=4.53=1.5(米).
答：浮漂B与河堤下端C之间的距离为1.5米.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，A，B两点在数轴上对应的数分别为a，b，且点A在点B的左边，|a|=10，a+b=80，ab＜0．
（1）求出a，b的值；
（2）现有一只电子蚂蚁P从点A出发，以3个单位长度/秒的速度向右运动，同时另一只电子蚂蚁Q从点B出发，以2个单位长度/秒的速度向左运动．
①设两只电子蚂蚁在数轴上的点C相遇，求出点C对应的数是多少？
②经过多长时间两只电子蚂蚁在数轴上相距20个单位长度？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，反比例函数y=
的图象与一次函数y=kx+b的图象交于点A，B，点A、B的横坐标分别为1，﹣2，一次函数图象与y轴的交于点C，与x轴交于点D．（1）求一次函数的解析式；
（2）对于反比例函数y=
，当y＜﹣1时，写出x的取值范围；（3）在第三象限的反比例图象上是否存在一个点P，使得S△ODP=2S△OCA？若存在，请求出点P的坐标；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】四座城市A,B,C,D分别位于一个边长100km的大正方形的四个顶点，由于各城市之间的商业往来日益频繁，于是政府决定修建公路网连接它们，根据实际，公路总长设计得越短越好，公开招标的信息发布后，一个又一个方案被提交上来，经过初审后，拟从下面四个方案中选定一个再进一步认证，其中符合要求的方案是（ ）
A. B. C. D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，∠ACB= 90°，CD是∠ACB的平分线，CD的垂直平分线分别交AC，CD，BC于点E ，O，F.求证:四边形CEDF是正方形.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，矩形纸片ABCD的长AD=9 cm，宽AB=3 cm，将其沿EF折叠，使点D与点B重合.
（1）求证:DE=BF;
（2）求BF的长.
-
科目： 来源： 题型：
查看答案和解析>>【题目】某工厂生产的某种产品按质量分为10个档次，第1档次（最低档次）的产品一天能生产95件，每件利润6元．每提高一个档次，每件利润增加2元，但一天产量减少5件．
（1）若生产第
档次的产品一天的总利润为
元（其中
为正整数，且1≤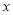
≤10），求出
关于
的函数关系式；（2）若生产第x档次的产品一天的总利润为1120元，求该产品的质量档次．
相关试题
