搜索
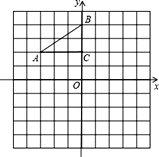
【题目】如图，在平面直角坐标系中，Rt△ABC的三个顶点分别是A（﹣3，2），B（0，4），C（0，2）．
（1）将△ABC以点C为旋转中心旋转180°，画出旋转后对应的△A1B1C1，平移△ABC，若点A的对应点A2的坐标为（0，﹣4），画出平移后对应的△A2B2C2；
（2）若将△A1B1C1绕某一点旋转可以得到△A2B2C2，请直接写出旋转中心的坐标．
参考答案：
【答案】（1）图形见解析；（2）P点坐标为（
，﹣1）．
【解析】
（1）分别作出点A、B关于点C的对称点，再顺次连接可得；由点A的对称点A2的位置得出平移方向和距离，据此作出另外两个点的对应点，顺次连接可得；
（2）连接A1A2、B1B2，交点即为所求．
（1）如图所示：A1（3，2）、C1（0，2）、B1（0，0）；A2（0，-4）、B2（3，﹣2）、C2（3，﹣4）．
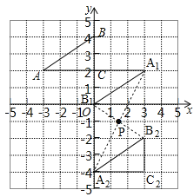
（2）将△A1B1C1绕某一点旋转可以得到△A2B2C2，旋转中心的P点坐标为（，﹣1）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】问题：探究函数的图象与性质．小华根据学习函数的经验，对函数的图象与性质进行了探究．下面是小华的探究过程，请补充完整：在函数y＝|x|﹣2中，自变量x可以是任意实数；
Ⅰ如表是y与x的几组对应值．
y
…
﹣3
﹣2
﹣1
0
1
2
3
…
x
…
1
0
﹣1
﹣2
﹣1
0
m
…
①m＝ ；
②若A（n，8），B（10，8）为该函数图象上不同的两点，则n＝ ；
Ⅱ如图，在平面直角坐标系xOy中，描出以上表中各对对应值为坐标的点．并根据描出的点，画出该函数的图象；根据函数图象可得：
①该函数的最小值为 ；
②该函数的另一条性质是 ．
-
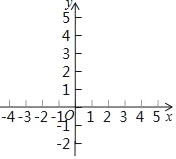
科目： 来源： 题型：
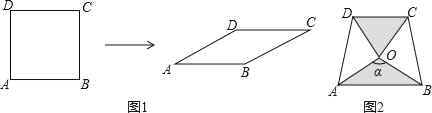
查看答案和解析>>【题目】如图1，将边长为1的正方形ABCD压扁为边长为1的菱形ABCD．在菱形ABCD中，∠A的大小为α，面积记为S．
（1）请补全表：
α
30°
45°
60°
90°
120°
135°
150°
S
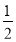
1
（2）填空：
由（1）可以发现单位正方形在压扁的过程中，菱形的面积随着∠A大小的变化而变化，不妨把单位菱形的面积S记为S（α）．例如：当α＝30°时，S＝S（30°）＝
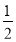；当α＝135°时，S＝S（135°）＝．由上表可以得到S（60°）＝S（ °）；S（150°）＝S（ °），…，由此可以归纳出S（180°﹣α）＝（ °）．（3）两块相同的等腰直角三角板按图2的方式放置，AD＝
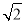，∠AOB＝α，试探究图中两个带阴影的三角形面积是否相等，并说明理由（注：可以利用（2）中的结论）． -
科目： 来源： 题型：
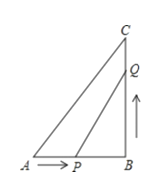
查看答案和解析>>【题目】如图，在△ABC中，∠B＝90°，AB＝6cm，BC＝8cm，动点P从点A开始沿AB边向B以1cm/s的速度移动（不与点B重合）；动点Q从B点开始沿BC边向点C以2cm/s的速度移动（不与点C重合）．如果P、Q分别从A、B同时出发，出发多少秒后，四边形APQC的面积为16cm2？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，∠C=90°，点O在AC上，以OA为半径的⊙O交AB于点D，BD的垂直平分线交BC于点E，交BD于点F，连接DE．
（1）判断直线DE与⊙O的位置关系，并说明理由；
（2）若AC=6，BC=8，OA=2，求线段DE的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，P为反比例函数y=
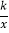（k＞0）在第一象限内图象上的一点，过点P分别作x轴，y轴的垂线交一次函数y=﹣x﹣4的图象于点A、B．若∠AOB=135°，则k的值是（ ）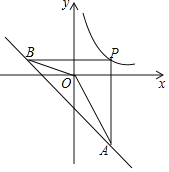
A. 2 B. 4 C. 6 D. 8
-
科目： 来源： 题型：
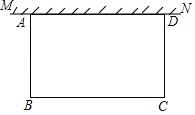
查看答案和解析>>【题目】如图，在足够大的空地上有一段长为a米的旧墙MN，某人利用旧墙和木栏围成一个矩形菜园ABCD，其中AD≤MN，已知矩形菜园的一边靠墙，另三边一共用了100米木栏．
（1）若a=20，所围成的矩形菜园的面积为450平方米，求所利用旧墙AD的长；
（2）求矩形菜园ABCD面积的最大值．
相关试题
