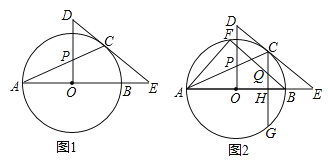
【题目】如图1,AB是⊙O的直径,E是AB延长线上一点,EC切⊙O于点C,OP⊥AO交AC于点P,交EC的延长线于点D.
(1)求证:△PCD是等腰三角形;
(2)CG⊥AB于H点,交⊙O于G点,过B点作BF∥EC,交⊙O于点F,交CG于Q点,连接AF,如图2,若sinE=![]() ,CQ=5,求AF的值.
,CQ=5,求AF的值.
参考答案:
【答案】(1)证明见解析;(2)12.
【解析】
试题分析:(1)连接OC,由切线性质和垂直性质得∠1+∠3=90°、∠2+∠4=90°,继而可得∠3=∠5得证;
(2)连接OC、BC,先根据切线性质和平行线性质及垂直性质证∠BCG=∠QBC得QC=QB=5,而sinE=sin∠ABF=![]() ,可知QH=3、BH=4,设圆的半径为r,在RT在△OCH中根据勾股定理可得r的值,在RT△ABF中根据三角函数可得答案.
,可知QH=3、BH=4,设圆的半径为r,在RT在△OCH中根据勾股定理可得r的值,在RT△ABF中根据三角函数可得答案.
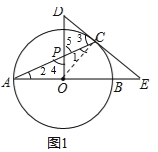
试题解析:(1)连接OC,∵EC切⊙O于点C,∴OC⊥DE,∴∠1+∠3=90°,又∵OP⊥OA,∴∠2+∠4=90°,∵OA=OC,∴∠1=∠2,∴∠3=∠4,又∵∠4=∠5,∴∠3=∠5,∴DP=DC,即△PCD为等腰三角形;
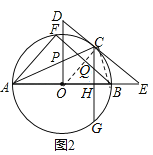
(2)如图2,连接OC、BC.∵DE与⊙O相切于点E,∴∠OCB+∠BCE=90°,∵OC=OB,∴∠OCB=∠OBC,∴∠OBC+∠BCE=90°,又∵CG⊥AB,∴∠OBC+∠BCG=90°,∴∠BCE=∠BCG,∵BF∥DE,∴∠BCE=∠QBC,∴∠BCG=∠QBC,∴QC=QB=5,∵BF∥DE,∴∠ABF=∠E,∵sinE=![]() ,∴sin∠ABF=
,∴sin∠ABF=![]() ,∴QH=3、BH=4,设⊙O的半径为r,∴在△OCH中,
,∴QH=3、BH=4,设⊙O的半径为r,∴在△OCH中,![]() ,解得:r=10,又∵∠AFB=90°,sin∠ABF=
,解得:r=10,又∵∠AFB=90°,sin∠ABF=![]() ,∴AF=12.
,∴AF=12.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x=﹣1是一元二次方程x2+mx+2m+3=0的一个根,求方程的另一个根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=kx+5的图象可由正比例函数y=2x的图象向上平移5个单位长度得到,则k=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果m+1的相反数是-7,则m的相反数是____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值3a(2a2﹣4a+3)﹣2a2(3a+4),其中a=﹣2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种蔬菜按品质分成三个等级销售,销售情况如下表:
等级
单价(元/千克)
销售量(千克)
一等
5.0
20
二等
4.5
40
三等
4.0
40
则售出蔬菜的平均单价为________元/千克.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x2=2x的解为________.
相关试题

