【题目】已知,∠AOB=90°,点C在射线OA上,CD∥OE.
(1)如图1,若∠OCD=120°,求∠BOE的度数;
(2)把“∠AOB=90°”改为“∠AOB=120°”,射线OE沿射线OB平移,得O′E,其他条件不变,(如图2所示),探究∠OCD、∠BO′E的数量关系;
(3)在(2)的条件下,作PO′⊥OB垂足为O′,与∠OCD的平分线CP交于点P,若∠BO′E=α,请用含α的式子表示∠CPO′(请直接写出答案).
参考答案:
【答案】(1)150°;(2)30°+![]() α.
α.
【解析】分析:(1)先根据平行线的性质得到∠AOE的度数,再根据直角、周角的定义即可求得∠BOE的度数;
(2)如图2,过O点作OF∥CD,根据平行线的判定和性质可得∠OCD、∠BO′E的数量关系;
(3)根据四边形内角和为360°,再根据(2)的结论,以及角平分线的定义即可求解.
详解:(1)∵CD∥OE,
∴∠AOE=∠OCD=120°,
∴∠BOE=360°-90°-120°=150°;

(2)如图2,过O点作OF∥CD,
∵CD∥OE,
∴OF∥OE,
∴∠AOF=180°-∠OCD,∠BOF=∠EO′O=180°-∠BO′E,
∴∠AOB=∠AOF+∠BOF=180°-∠OCD+180°-∠BO′E=360°-(∠OCD+∠BO′E)=120°,
∴∠OCD+∠BO′E=240°;
(3)∵CP是∠OCD的平分线,
∴∠OCP=![]() ∠OCD,
∠OCD,
∴∠CPO′=360°-90°-120°-∠OCP
=150°-![]() ∠OCD
∠OCD
=150°-![]() (240°-∠BO′E)
(240°-∠BO′E)
=30°+![]() α.
α.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.

(1)求证:Rt△ABE≌Rt△CBF;
(2)若∠CAE=30°,求∠ACF的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各式因式分解:
(1)
 (2)
(2)
(3)
 (4)
(4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】将点Q(2, -1)向右平移2个单位,再向下平移3个单位得到点R的坐标是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察分析下列方程:①
 ,②
,② 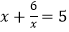 ,③
,③  ;请利用它们所蕴含的规律,求关于x的方程
;请利用它们所蕴含的规律,求关于x的方程  (n为正整数)的根,你的答案是: .
(n为正整数)的根,你的答案是: . -
科目: 来源: 题型:
查看答案和解析>>【题目】北京奥运会体育场的“鸟巢”钢结构工程施工建设中,首次使用了我国科研人员自主研制的强度为4.6×108帕的钢材,那么它的原数是( )
A.4600000B.46000000C.460000000D.4600000000
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依次为2,4,6,8,…,顶点依次用
 ,
, ,
, ,
, …表示,则顶点
…表示,则顶点 的坐标是_____.
的坐标是_____.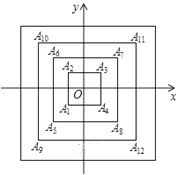
相关试题

