【题目】如图,将矩形ABCD沿对角线AC翻折,点B落在点E处,EC交AD于F.
(1)求证:△AEF≌△CDF;
(2)若AB=4,BC=8,EF=3,求图中阴影部分的面积。

参考答案:
【答案】(1)见解析;(2)10.
【解析】(1)根据矩形性质和折叠性质可得:∠E=∠D,∠AFE=∠CFD,AE=CD,
故△AEF≌△CDF(AAS);
(2)结合(1)可得阴影部分的面积=S△ADC-S△FDC=![]() AD·DC-
AD·DC-![]() FD·DC,代入已知数可得.
FD·DC,代入已知数可得.
解:(1)∵四边形ABCD是矩形,
∴AB=CD,∠B=∠D=90,
∵将矩形ABCD沿对角线AC翻折,点B落在点E处,
∴∠E=∠B,AB=AE,
∴AE=CD,∠E=∠D,
在△AEF与△CDF中,
∠E=∠D,∠AFE=∠CFD,AE=CD,
∴△AEF≌△CDF(AAS);
(2)根据(1)得:△AEF≌△CDF,EF=3
∴DF=EF=3
∵AB=4,BC=8,
∴AD=BC=8, CD=AB=4
∴阴影部分的面积=S△ADC-S△FDC=![]() AD·DC-
AD·DC-![]() FD·DC
FD·DC
=![]() ×8×4-
×8×4-![]() ×3×4
×3×4
=16-6=10
-
科目: 来源: 题型:
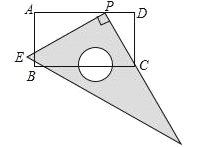
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=6,AD=11.直角尺的直角顶点P在AD上滑动时(点P与A,D不重合),一直角边始终经过点C,另一直角边与AB交于点E.
(1)△CDP与△PAE相似吗?如果相似,请写出证明过程;
(2)是否存在这样的点P,使△CDP的周长等于△PAE周长的2倍?若存在,求DP的长;若不存在,请说明理由.
-
科目: 来源: 题型:
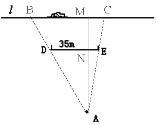
查看答案和解析>>【题目】如示意图,小华家(点A处)和公路(l)之间竖立着一块35m长且平行于公路的巨型广告牌(DE).广告牌挡住了小华的视线,请在图中画出视点A的盲区,并将盲区内的那段公路计为BC.一辆以60km/h匀速行驶的汽车经过公路段的时间是3s,已知广告牌和公路的距离是40m,求小华家到公路的距离.(精确到1m)
-
科目: 来源: 题型:
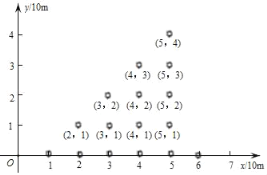
查看答案和解析>>【题目】某景区有一片树林,不仅树种相同,而且排列有序,如果用平面直角坐标系来表示每一棵的具体位置,从第一棵树开始依次表示为(1,0)→(2,0)→(2,1)→(3,2)→(3,1)→(3,0)→(4.0)→……,则第100棵树的位置是____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一个坡角为30°的斜坡上有一电线杆AB,当太阳光与水平线成45°角时,测得该杆在斜坡上的影长BC为20m.求电线杆AB的高(精确到0.1m,参考数值:
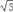 ≈1.73,
≈1.73,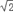 ≈1.41).
≈1.41).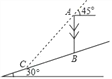
-
科目: 来源: 题型:
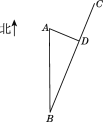
查看答案和解析>>【题目】如图,某沿海城市A接到台风警报,在该城市正南方向260 km的B处有一台风中心,沿BC方向以15 km/h的速度向C移动,已知城市A到BC的距离AD=100 km,那么台风中心经过多长时间从B点移动到D点?如果在距台风中心30 km的圆形区域内都将受到台风的影响,正在D点休息的游人在接到台风警报后的几小时内撤离才可以免受台风的影响?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店以每件20元的价格购进一批商品,如果以每件30元销售,那么半月内可售出400件.根据销售经验,销售单价每提高1元,半月内的销售量相应减少20件.如何提高销售单价,才能在半月内获得最大利润?最大利润是多少?
相关试题

