【题目】如图1,AB=BC=CD=DA,∠A=∠B=∠BCD=∠ADC=90°,点E是AB上一点,点F是AD延长线上一点,且DF=BE.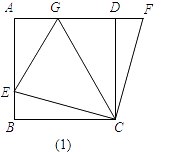
(1)求证:CE=CF;
(2)在图1中,如果点G在AD上,且∠GCE=45°,那么EG=BE+DG是否成立,请说明理由.
(3)运用(1)、(2)解答中所积累的经验和知识,完成下题:如图2,AD∥BC(BC>AD),∠B=90°,AB=BC=12,点E是AB上一点,且∠DCE=45°,BE=4,求DE的长.
参考答案:
【答案】
(1)
证明:在△CBE和△CDF中,
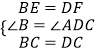 ,
,
∴△CBE≌△CDF,
∴CE=CF;
(2)
解:EG=BE+DG成立,
∵△CBE≌△CDF,
∴CE=CF,∠BCE=∠DCF,BE=DF,
∵∠BCD=90°,∠GCE=45°,
∴∠BCE+∠DCG=45°,
∴∠DCF+∠DCG=45°,即∠FCG=45°,
∴∠FCG=∠GCE,
在△ECG和△FCG中,
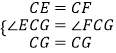 ,
,
∴△ECG≌△FCG,
∴GE=GF,
∴EG=BE+DG;
(3)
作CF⊥AD交AD的延长线于F,
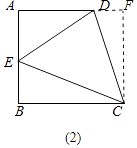
由(2)得,DE=BE+DF,
设DE=x,
∵AB=12,BE=4,
∴AE=8,
∴DF=x﹣4,AD=12﹣(x﹣4)=16﹣x,
由勾股定理得,82+(16﹣x)2=x2,
解得,x=10,
∴DE的长为10.
【解析】(1)证明△CBE≌△CDF,根据全等三角形的性质证明;(2)根据全等三角形的性质得到CE=CF,∠BCE=∠DCF,BE=DF,证明△ECG≌△FCG,根据全等三角形的性质解答;(3)根据(2)的结论和勾股定理计算即可.
-
科目: 来源: 题型:
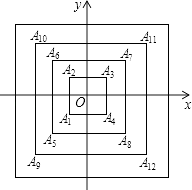
查看答案和解析>>【题目】如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行.从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A1 , A2 , A3 , A4 , …表示,则顶点A55的坐标是( )
A.(13,13)
B.(﹣13,﹣13)
C.(14,14)
D.(﹣14,﹣14) -
科目: 来源: 题型:
查看答案和解析>>【题目】写出一个两根分别为0和2的一元二次方程:___.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2013年第一季度,泰州市共完成工业投资22300000000元,22300000000这个数可用科学记数法表示为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于一次函数y=x+6,下列结论错误的是( )
A.函数值随自变量增大而增大
B.函数图象与x轴正方向成45°角
C.函数图象不经过第四象限
D.函数图象与x轴交点坐标是(0,6) -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A的坐标为(1,2),将点A向右平移3个单位长度后得到点A′,则点A′的坐标是( )
A. (-2,2) B. (1,5) C. (1,-1) D. (4,2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】将点A(1,1)先向左平移2个单位长度,再向下平移3个单位长度得到点B,则点B的坐标是______.
相关试题

