【题目】如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,连接BD
(1)求证:BD平分∠ABC;
(2)当∠ODB=30°时,求证:BC=OD.
参考答案:
【答案】
(1)
∵OD⊥AC OD为半径,∴ ![]() ,
,
∴∠CBD=∠ABD,
∴BD平分∠ABC;
(2)
证明:∵OB=OD,
∴∠OBD=∠0DB=30°,
∴∠AOD=∠OBD+∠ODB=30°+30°=60°,
又∵OD⊥AC于E,
∴∠OEA=90°,
∴∠A=180°﹣∠OEA﹣∠AOD=180°﹣90°﹣60°=30°,
又∵AB为⊙O的直径,
∴∠ACB=90°,
在Rt△ACB中,BC= ![]() AB,
AB,
∵OD= ![]() AB,
AB,
∴BC=OD
【解析】(1)由OD⊥AC OD为半径,根据垂径定理,即可得 ![]() ,又由在同圆或等圆中,同弧或等弧所对的圆周角相等,即可证得BD平分∠ABC;(2)首先由OB=OD,易求得∠AOD的度数,又由OD⊥AC于E,可求得∠A的度数,然后由AB是⊙O的直径,根据圆周角定理,可得∠ACB=90°,继而可证得BC=OD.
,又由在同圆或等圆中,同弧或等弧所对的圆周角相等,即可证得BD平分∠ABC;(2)首先由OB=OD,易求得∠AOD的度数,又由OD⊥AC于E,可求得∠A的度数,然后由AB是⊙O的直径,根据圆周角定理,可得∠ACB=90°,继而可证得BC=OD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,将△ABC纸片沿中位线EH折叠,使点A对称点D落在BC边上,再将纸片分别沿等腰△BED和等腰△DHC的底边上的高线EF,HG折叠,折叠后的三个三角形拼合形成一个矩形,类似地,对多边形进行折叠,若翻折后的图形恰能拼合成一个无缝隙、无重叠的矩形,这样的矩形称为叠合矩形.




(1)将□ABCD纸片按图2的方式折叠成一个叠合矩形AEFG,则操作形成的折痕分别是线段_______,_________;S矩形AEFG:S□ABCD=__________.
(2)□ABCD纸片还可以按图3的方式折叠成一个叠合矩形EFGH,若EF=5,EH=12,求AD的长;
(3)如图4,四边形ABCD纸片满足AD∥BC,AD<BC,AB⊥BC,AB=8,CD=10,小明把该纸片折叠,得到叠合正方形,请你帮助画出一种叠合正方形的示意图,并求出AD、BC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了提高沈城市民的节水意识,有关部门就“你认为最有效的节水措施”随机对部分市民进行了问卷调查,其中问卷设置以下选项(被调查者只能选择其中的一项)A.出台相关法律法规 B.控制用水大户数量 C.推广节水技改和节水器具 D.用水量越多,水价越高. E.其他
根据调查结果制作了统计图表的一部分如下: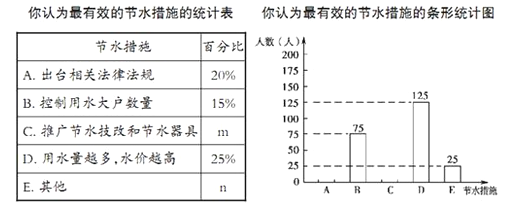
(1)此次抽样调查的人数为人;
(2)结合上述统计图表可得m=;n= .
(3)请根据以上信息直接补全条形统计图. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人加工同一种机器零件,甲比乙每小时多加工10个零件,甲加工150个零件所用的时间与乙加工120个零件所用时间相等
(1)求甲、乙两人每小时各加工多少个机器零件? -
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)(- 5)+ 6
(2)(+21)+(-31)
(3)(- 5.2 ) + ( - 1.2 )
(4)(﹣3)+7+(﹣6)+(﹣7)
(5)(- 20 ) +(-14)+(-28)+16
(6)5.6+(﹣0.9)+4.4+(﹣8.1)
(7)30 + 15+(-7)+(-15)
(8)
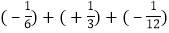 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个正方体的六个面上写有六个连续的整数.如图,是此正方体的展开图,相对面上两个数之和相等,且
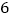 个整数之和为
个整数之和为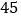 ,则
,则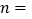 ________.
________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD中,对角线AC和BD相交于点O,如果AC=12、BD=10、AB=m,那么m的取值范围是( )

A. 1<m<11 B. 2<m<22 C. 10<m<12 D. 5<m<6
相关试题

