【题目】如图矩形ABCD中,AB=12,BC=8,E、F分别为AB、CD的中点,点P、Q从A. C同时出发,在边AD、CB上以每秒1个单位向D、B运动,运动时间为t(0<t<8).
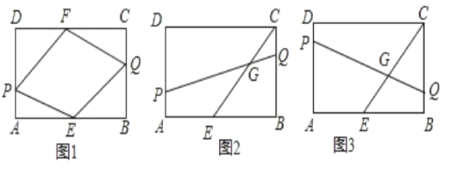
(1)如图1,连接PE、EQ、QF、PF,求证:无论t在0<t<8内取任何值,四边形PEQF总为平行四边形;
(2)如图2,连接PQ交CE于G,若PG=4QG,求t的值;
(3)在运动过程中,是否存在某时刻使得PQ⊥CE于G?若存在,请求出t的值:若不存在,请说明理由
参考答案:
【答案】(1)见解析;(2)![]() ;(3)不存在,理由见解析.
;(3)不存在,理由见解析.
【解析】
(1)由矩形的性质得出CD=AB=12,AD=BC=8,∠A=∠B=∠C=∠D=90°,由SAS证明△APE≌△CQF,得出PE=QF,同理:PF=QE,即可得出结论;
(2)根据题意得:AP=CQ=t,∴PD=QB=8-t,作EF∥BC交CD于E,交PQ于H,证出EH是梯形ABQP的中位线,由梯形中位线定理得出EH=![]() (AP+BQ)=4,证出GH:GQ=3:2,由平行线得出△EGH∽△CGQ,得出对应边成比例
(AP+BQ)=4,证出GH:GQ=3:2,由平行线得出△EGH∽△CGQ,得出对应边成比例![]() ,即可得出t的值;
,即可得出t的值;
(3)由勾股定理求出CE=![]() =10,作EM∥BC交PQ于M,由(2)得:ME=4,证出△GCQ∽△BCE,得出对应边成比例求出CG=t
=10,作EM∥BC交PQ于M,由(2)得:ME=4,证出△GCQ∽△BCE,得出对应边成比例求出CG=t![]() ,得出EG=10-
,得出EG=10-![]() t,由平行线证明△GME∽△GQC,得出对应边成比例,求出t=0或t=8.5,即可得出结论.
t,由平行线证明△GME∽△GQC,得出对应边成比例,求出t=0或t=8.5,即可得出结论.
(1)证明:∵四边形ABCD是矩形,
∴CD=AB=12,AD=BC=8,∠A=∠B=∠C=∠D=90°,
∵E、F分别为AB、CD的中点,
∴AE=BE=6,DF=CF=6,
∴AE=BE=DF=CF,
∵点P、Q从A. C同时出发,在边AD、CB上以每秒1个单位向D、B运动,
∴AP=CQ=t,
在△APE和△CQF中,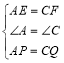 ,
,
∴△APE≌△CQF(SAS),
∴PE=QF,
同理:PF=QE,
∴四边形PEQF总为平行四边形;
(2)根据题意得:AP=CQ=t,
∴PD=QB=8t,
作EF∥BC交CD于E,交PQ于H,如图2所示:
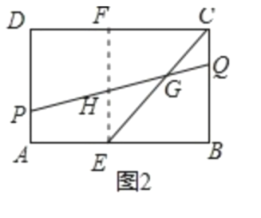
则F为CD的中点,H为PQ的中点,EF=BC=8,
∴EH是梯形ABQP的中位线,
∴EH=![]() (AP+BQ)=4,
(AP+BQ)=4,
∵PG=4QG,
∴GH:GQ=3:2,
∵EF∥BC,
∴△EGH∽△CGQ,
∴![]() =
=![]() ,即4t=
,即4t=![]() ,
,
解得:t=![]() ,
,
∴若PG=4QG,t的为![]() 值;
值;
(3)不存在,理由如下:
∵∠B=90°,BE=6,BC=8,
∴CE=![]() =10,
=10,
作EM∥BC交PQ于M,如图3所示:
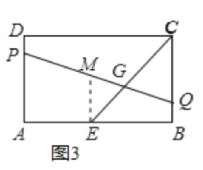
由(2)得:ME=4,
∵PQ⊥CE,
∴∠CGQ=90°=∠B,
∵∠GCQ=∠BCE,
∴△GCQ∽△BCE,
∴![]() ,即
,即![]() =
=![]() ,
,
∴CG=![]() t,
t,
∴EG=10![]() t,
t,
∵EM∥BC,
∴△GME∽△GQC,
∴![]() ,即
,即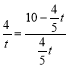 ,
,
解得:t=0或t=8.5,
∵0<t<8,
∴不存在。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数y=
 x3与反比例函数y=
x3与反比例函数y= 的图象相交于点A(4,n),与x轴相交于点B.
的图象相交于点A(4,n),与x轴相交于点B.
(1)填空:n的值为___,k的值为___;
(2)以AB为边作菱形ABCD,使点C在x轴正半轴上,点D在第一象限,求点D的坐标;
(3)观察反比例函数y=
 的图象,当y2时,请直接写出自变量x的取值范围。
的图象,当y2时,请直接写出自变量x的取值范围。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,在数轴上有A,B两点,所表示的数分别为-10,4,点A以每秒5个单位长度的速度向右运动,同时点B以每秒3个单位长度的速度也向左运动,如果设运动时间为t秒,解答下列问题:

(1)运动前线段AB的长为 ; 运动1秒后线段AB的长为 ;
(2)运动t秒后,点A,点B运动的距离分别为 ;用t表示A,B分别为 .
(3)求t为何值时,点A与点B恰好重合;
(4)在上述运动的过程中,是否存在某一时刻t,使得线段AB的长为6,若存在,求t的值; 若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个几何体是由若干个棱长为3cm的小正方体搭成的,从左面、上面看到的几何体的形状图如图所示:
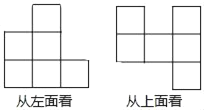
(1)该几何体最少由 个小立方体组成,最多由 个小立方体组成.
(2)将该几何体的形状固定好,
①求该几何体体积的最大值;
②若要给体积最小时的几何体表面涂上油漆,求所涂油漆面积的最小值.
-
科目: 来源: 题型:
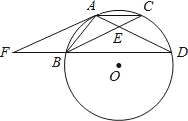
查看答案和解析>>【题目】如图,点A,B,C,D在⊙O上,AB=AC,AD与BC相交于点E,AE=
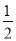 ED,延长DB到点F,使FB=
ED,延长DB到点F,使FB=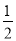 BD,连接AF.
BD,连接AF.(1)证明:△BDE∽△FDA;
(2)试判断直线AF与⊙O的位置关系,并给出证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知O是AB上的一点,从O点引出射线OC、OE、OD,其中OE平分∠BOC.
(1)如图1,若∠COD是直角,∠DOE=15°,求∠AOE的度数;
(2)如图1,若∠AOC=∠BOD,∠DOE=15°,求∠AOE的度数;
(3)将图1中的∠COD (∠COD仍是直角)绕顶点O顺时针旋转至图2的位置,若∠AOC=
 , ∠DOE=
, ∠DOE= ,请猜想
,请猜想 与
与 之间存在什么样的数量关系,写出你的结论,并说明理由.
之间存在什么样的数量关系,写出你的结论,并说明理由. 
-
科目: 来源: 题型:
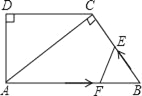
查看答案和解析>>【题目】如图,在直角梯形ABCD中,AB∥DC,∠D=90°,AC⊥BC,AB=10cm,BC=6cm,F点以2cm/秒的速度在线段AB上由A向B匀速运动,E点同时以1cm/秒的速度在线段BC上由B向C匀速运动,设运动时间为t秒(0<t<5).
(1)求证:△ACD∽△BAC;
(2)求DC的长;
(3)设四边形AFEC的面积为y,求y关于t的函数关系式,并求出y的最小值.
相关试题

