【题目】如图在△ABC中,AD⊥BC,垂足为D,E是AC边上一点,BE与AD交于点F,若∠ABC=45°,∠BAC=75°,∠BFD=60°.求∠BEC的度数.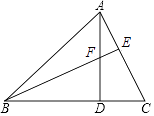
参考答案:
【答案】解:∵AD⊥BC,
∴∠FDB=90°.
∵∠BFD=60°,
∴∠FBD=90°﹣60°=30°.
在△ABC中,
∵∠ABC=45°,∠BAC=75°,
∴∠C=180°﹣∠ABC﹣∠BAC=180°﹣45°﹣75°=60°.
在△BEC中,∵∠FBD=30°,∠C=60°,
∴∠BEC=180°﹣∠FBD﹣∠C=180°﹣30°﹣60°=90°.
【解析】先根据AD⊥BC得出∠FDB=90°,根据直角三角形的性质得出∠FBD的度数,再由三角形内角和定理得出∠C的度数,在△BEC中,根据∠BEC=180°-∠FBD-∠C即可得出结论.
【考点精析】本题主要考查了三角形的内角和外角的相关知识点,需要掌握三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】每年5月的第二周为“职业教育活动周”,今年我省开展了以“弘扬工匠精神,打造技能强国”为主题的系列活动.活动期间某职业中学组织全校师生并邀请学生家长和社区居民参加“职教体验观摩”活动,相关职业技术人员进行了现场演示,活动后该校教务处随机抽取了部分学生进行调查:“你最感兴趣的一种职业技能是什么?”并对此进行了统计,绘制了统计图(均不完整).请解答以下问题:
(1)补全条形统计图和扇形统计图;
(2)若该校共有1800名学生,请估计该校对“工业设计”最感兴趣的学生有多少人?
(3)要从这些被调查的学生中,随机抽取一人进行访谈,那么正好抽到对“机电维修”最感兴趣的学生的概率是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知5b-2a-2=7a-4b,则a,b的大小关系是______ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】到直线L的距离等于2cm的点有( )
A. 0个 B. 2个 C. 3个 D. 无数个
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种商品进货后,零售价定为每件900元,为了适应市场竞争,商店按零售价的九折降价,并让利40元销售,仍可获利10%(相对于进价),问这种商品的进价为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年5月,某大型商业集团随机抽取所属的m家商业连锁店进行评估,将各连锁店按照评估成绩分成了A、B、C、D四个等级,绘制了如图尚不完整的统计图表.

根据以上信息解答下列问题:
(1)求m的值;
(2)在扇形统计图中,求B等级所在扇形的圆心角的大小;(结果用度、分、秒表示)
(3)从评估成绩不少于80分的连锁店中任选2家介绍营销经验,求其中至少有一家是A等级的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】点P与Q(﹣2,3)关于x轴对称,则线段PQ的长为_____.
相关试题

