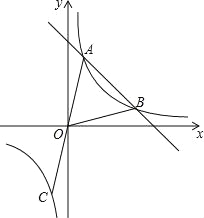
【题目】如图,直线y=﹣x+b与反比例函数![]() 的图象相交于A(1,4),B两点,延长AO交反比例函数图象于点C,连接OB.
的图象相交于A(1,4),B两点,延长AO交反比例函数图象于点C,连接OB.
(1)求k和b的值;
(2)直接写出一次函数值小于反比例函数值的自变量x的取值范围;
(3)在y轴上是否存在一点P,使![]() ?若存在请求出点P坐标,若不存在请说明理由.
?若存在请求出点P坐标,若不存在请说明理由.
参考答案:
【答案】(1)b=5,k=4(2)x>4或0<x<1(3)P(0,3)或P(0,﹣3)
【解析】
试题分析:(1)由待定系数法即可得到结论;
(2)根据图象中的信息即可得到结论;
(3)过A作AM⊥x轴,过B作BN⊥x轴,由(1)知,b=5,k=4,得到直线的表达式为:y=﹣x+5,反比例函数的表达式为:![]() 列方程
列方程![]() ,求得B(4,1),于是得到
,求得B(4,1),于是得到![]() ,由已知条件得到
,由已知条件得到![]() ,过A作AE⊥y轴,过C作CD⊥y轴,设P(0,t),根据三角形的面积公式列方程即可得到结论.
,过A作AE⊥y轴,过C作CD⊥y轴,设P(0,t),根据三角形的面积公式列方程即可得到结论.
试题解析:(1)将A(1,4)分别代入y=﹣x+b和![]()
得:4=﹣1+b,4=![]() ,解得:b=5,k=4;
,解得:b=5,k=4;
(2)一次函数值小于反比例函数值的自变量x的取值范围为:x>4或0<x<1,
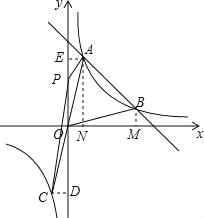
(3)过A作AM⊥x轴,过B作BN⊥x轴,
由(1)知,b=5,k=4,
∴直线的表达式为:y=﹣x+5,反比例函数的表达式为:![]()
由![]() ,解得:x=4,或x=1,
,解得:x=4,或x=1,
∴B(4,1),
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
过A作AE⊥y轴,过C作CD⊥y轴,设P(0,t),
∴S△PAC=![]() OPCD+
OPCD+![]() OPAE=
OPAE=![]() OP(CD+AE)=|t|=3,
OP(CD+AE)=|t|=3,
解得:t=3,t=﹣3,
∴P(0,3)或P(0,﹣3).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上,已知在纸面上有一数轴(如图),折叠纸面.
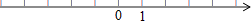
(1)若1表示的点与﹣1表示的点重合,则﹣2表示的点与数表示的点重合;
(2)若﹣1表示的点与3表示的点重合,5表示的点与数表示的点重合;
(3)若数轴上A、B两点之间的距离为c个单位长度,点A表示的有理数是a,并且A、B两点经折叠后重合,请写出此时折线与数轴的交点表示的有理数是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】问题引入:
(1)如图1,在△ABC中,点O是∠ABC和∠ACB平分线的交点,若∠A=α,则∠BOC= (用α表示);
如图2,∠CBO=
 ∠ABC,∠BCO=
∠ABC,∠BCO= ∠ACB,∠A=α,则∠BOC= (用α表示);
∠ACB,∠A=α,则∠BOC= (用α表示);拓展研究:
(2)如图3,∠CBO=
 ∠DBC,∠BCO=
∠DBC,∠BCO= ∠ECB,∠A=α,猜想∠BOC= (用α表示),并说明理由;
∠ECB,∠A=α,猜想∠BOC= (用α表示),并说明理由;(3)BO、CO分别是△ABC的外角∠DBC、∠ECB的n等分线,它们交于点O,∠CBO=
 ∠DBC,∠BCO=
∠DBC,∠BCO= ∠ECB,∠A=α,请猜想∠BOC= .
∠ECB,∠A=α,请猜想∠BOC= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简x-y-(x+y)的最后结果是( )
A.0
B.2x
C.-2y
D.2x-2y -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)﹣9+(+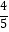 )﹣(﹣12)+(﹣5)+(﹣
)﹣(﹣12)+(﹣5)+(﹣ 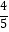 )
)
(2)(1﹣1 ﹣
﹣  +
+ 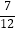 )×(﹣24)
)×(﹣24)
(3)﹣ +
+ 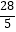 ÷(﹣2)×(﹣
÷(﹣2)×(﹣ 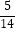 )
)
(4)﹣14﹣(1﹣ )÷3×|3﹣(﹣3)2|
)÷3×|3﹣(﹣3)2| -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀平均分成4个小长方形,然后按图2的形状拼成一个正方形.
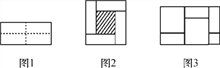
(1)图2中阴影部分的面积为 ;
(2)观察图2,请你写出式子(m+n)2,(m-n)2,mn之间的等量关系: ;
(3)若x+y=-6,xy=2.75,则x-y= ;
(4)实际上有许多恒等式可以用图形的面积来表示,如图3,它表示等式: .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,点P是⊙O外的一点,PB与⊙O相交于点A、B,PD与⊙O相交于C、D,AB=CD.
求证:(1)PO平分∠BPD;
(2)PA=PC.

相关试题

