【题目】(1)如图①,![]() 的内角
的内角![]() 的平分线与外角
的平分线与外角![]() 的平分线相交于
的平分线相交于![]() 点,
点,![]() ,求
,求![]() 的度数.
的度数.

(2)如图,四边形![]() 中,设
中,设![]() ,
,![]() ,
,![]() 为四边形
为四边形![]() 的内角
的内角![]() 与外角
与外角![]() 的平分线所在直线相交而形成的锐角.
的平分线所在直线相交而形成的锐角.
①如图②,若![]() ,求
,求![]() 的度数.(用
的度数.(用![]() 、
、![]() 的代数式表示)
的代数式表示)
②如图③,若![]() ,请在图③中画出
,请在图③中画出![]() ,并求得
,并求得![]() .(用
.(用![]() 、
、![]() 的代数式表示)
的代数式表示)

参考答案:
【答案】(1)∠P=20°
(2)①![]() ②
②![]()
【解析】
试题(1)根据角平分线的性质和三角形的外角的性质,可等量代换证明;
(2)①延长BA、CD交于点F,然后根据(1)的解题可得到规律;
②由上面的结论直接写出解答即可.
试题解析:(1)∵BP 平分∠ABC,CP 平分∠ACD
∴∠ABC=2∠PBC ,∠ACD=2∠PCD
∵∠ACD=∠A+∠ABC,∠PCD=∠P+∠PBC
∴2∠PCD=∠A+2∠PBC
∴2(∠P+∠PBC)=∠A+2∠PBC
∴∠P=![]()
∴∠P=20°
(2)①延长BA、CD交于点F,由(1)知∠P=![]()
∴![]() =
=![]()
②![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有甲、乙两个可以自由转动的转盘,其中转盘甲被平均分成三个扇形,转盘乙被平均分成五个扇形,小明与小亮玩转盘游戏,规则如下:同时转动两个转盘,转盘停止后,转盘中甲指针所指数字作为点的横坐标,转盘乙指针所指数字作为点的纵坐标,从而确定一个点的坐标为A(m,n).当点A在第一象限时,小明赢;当点A在第二象限时,小亮赢.请你利用画树状图或列表法分析该游戏规则对双方是否公平?并说明理由.
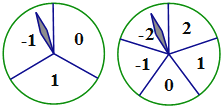
-
科目: 来源: 题型:
查看答案和解析>>【题目】去冬今春,我市部分地区遭受了罕见的旱灾,“旱灾无情人有情”.某单位给某乡中小学捐献一批饮用水和蔬菜共320件,其中饮用水比蔬菜多80件.
(1)求饮用水和蔬菜各有多少件?
(2)现计划租用甲、乙两种货车共8辆,一次性将这批饮用水和蔬菜全部运往该乡中小学.已知每辆甲种货车最多可装饮用水40件和蔬菜10件,每辆乙种货车最多可装饮用水和蔬菜各20件.则运输部门安排甲、乙两种货车时有几种方案?请你帮助设计出来;
(3)在(2)的条件下,如果甲种货车每辆需付运费400元,乙种货车每辆需付运费360元.运输部门应选择哪种方案可使运费最少?最少运费是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是⊙O的内接三角形且AB=AC,BD是⊙O的直径,过点A做AP∥BC交DB的延长线于点P,连接AD.
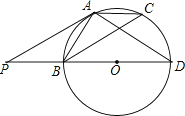
(1)求证:AP是⊙O的切线;
(2)若⊙O的半径是2,cos∠ABC= ,求AB的长.
,求AB的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,A(a,0),B(0,b),a,b满足
 =0,C为AB的中点,P是线段AB上一动点,D是x轴正半轴上一点,且PO=PD,DE⊥AB于E.
=0,C为AB的中点,P是线段AB上一动点,D是x轴正半轴上一点,且PO=PD,DE⊥AB于E.(1)求∠OAB的度数
(2)当点P运动时,PE的长是否变化?若变化,请说明理由;若不变,请求PE的长
(3)若∠OPD=45度,求点D的坐标

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某班研究性学习小组在一次综合实践活动中发现如下问题:在楼底的B处测得河对岸大厦上悬挂的条幅底端D的仰角为26°,在楼顶A处测得条幅顶端C的仰角为50°.若楼AB高度为18米,条幅CD长度为46米,请你帮助他们求出楼与大厦之间的距离BE及大厦的高度CE.(参考数据:sin26°≈0.44,sin50°≈0.77,tan26°≈0.49,tan50°≈1.19).
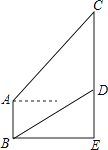
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场将进价为4000元的电视以4400元售出,平均每天能售出6台.为了配合国家财政推出的“节能家电补贴政策”的实施,商场决定采取适当的降价措施,调查发现:这种电视的售价每降价50元,平均每天就能多售出3台.
(1)现设每台电视降价x元,商场每天销售这种电视的利润是y元,请写出y与x之间的函数表达式.(不要求写出自变量的取值范围)
(2)每台电视降价多少元时,商场每天销售这种电视的利润最高?最高利润是多少?
(3)商场要想在这种电视销售中每天盈利3600元,同时又要使百姓得到更多实惠,每台电视应降价多少元?根据以上的结论,请你直接写出售价在什么范围时,每个月的利润不低于3600元?
相关试题

