【题目】如图1,点A、B分别在数轴原点O的左右两侧,且 ![]() OA+50=OB,点B对应数是90.
OA+50=OB,点B对应数是90. ![]()
(1)求A点对应的数;
(2)如图2,动点M、N、P分别从原点O、A、B同时出发,其中M、N均向右运动,速度分别为2个单位长度/秒,7个单位长度/秒,点P向左运动,速度为8个单位长度/秒,设它们运动时间为t秒,问当t为何值时,点M、N之间的距离等于P、M之间的距离; ![]()
(3)如图3,将(2)中的三动点M、N、P的运动方向改为与原来相反的方向,其余条件不变,设Q为线段MN的中点,R为线段OP的中点,求22RQ﹣28RO﹣5PN的值. ![]()
参考答案:
【答案】
(1)解:如图1,∵点B对应数是90,
∴OB=90.
又∵ ![]() OA+50=OB,即
OA+50=OB,即 ![]() OA+50=90,
OA+50=90,
∴OA=120.
∴点A所对应的数是﹣120
![]()
(2)解:依题意得,MN=|(﹣120+7t)﹣2t|=|﹣120+5t|,
PM=|2t﹣(90﹣8t)|=|10t﹣90|,
又∵MN=PM,
∴|﹣120+5t|=|10t﹣90|,
∴﹣120+5t=10t﹣90或﹣120+5t=﹣(10t﹣90)
解得t=﹣6或t=14,
∵t≥0,
∴t=14,点M、N之间的距离等于点P、M之间的距离
![]()
(3)解:依题意得RQ=( 45+4t)﹣(﹣60﹣4.5t)=105+8.5t,
RO=45+4t,
PN=(90+8t)﹣(﹣120﹣7t)=210+15t,
则22RQ﹣28RO﹣5PN=22(105+8.5t)﹣28(45+4t)﹣5(210+15t)=0
![]()
【解析】(1)根据点B对应的数求得OB的长度,结合已知条件和图形来求点A所对应的数;(2)由M、N之间的距离等于P、M之间的距离列式为,列方程求出t;(3)由M、N之间的距离等于P、M之间的距离列式为,列方程求出t,并求出RQ,RO及PN,再求出22RQ﹣28RO﹣5PN的值.
【考点精析】根据题目的已知条件,利用数轴和两点间的距离的相关知识可以得到问题的答案,需要掌握数轴是规定了原点、正方向、单位长度的一条直线;同轴两点求距离,大减小数就为之.与轴等距两个点,间距求法亦如此.平面任意两个点,横纵标差先求值.差方相加开平方,距离公式要牢记.
-
科目: 来源: 题型:
查看答案和解析>>【题目】地球上的海洋面积约三亿六千一百万平方千米,用科学记数法表示为( )平方千米.
A. 361×106B. 36.1×107C. 3.61×108D. 0.361×109
-
科目: 来源: 题型:
查看答案和解析>>【题目】“皮克定理”是用来计算顶点在整点的多边形面积的公式,公式表达式为S=a+
 ﹣1,孔明只记得公式中的S表示多边形的面积,a和b中有一个表示多边形边上(含顶点)的整点个数,另一个表示多边形内部的整点个数,但不记得究竟是a还是b表示多边形内部的整点个数,请你选择一些特殊的多边形(如图1)进行验证,得到公式中表示多边形内部的整点个数的字母是 , 并运用这个公式求得图2中多边形的面积是 .
﹣1,孔明只记得公式中的S表示多边形的面积,a和b中有一个表示多边形边上(含顶点)的整点个数,另一个表示多边形内部的整点个数,但不记得究竟是a还是b表示多边形内部的整点个数,请你选择一些特殊的多边形(如图1)进行验证,得到公式中表示多边形内部的整点个数的字母是 , 并运用这个公式求得图2中多边形的面积是 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:mn2+6mn+9m=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD 内接于⊙O,BD是⊙O的直径,过点A作AE⊥CD,交CD的延长线于点E,DA平分∠BDE.
(1)求证:AE是⊙O的切线;
(2)已知AE=4cm,CD=6cm,求⊙O的半径.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点A、B分别在数轴原点O的左右两侧,且
 OA+50=OB,点B对应数是90.
OA+50=OB,点B对应数是90. 
(1)求A点对应的数;
(2)如图2,动点M、N、P分别从原点O、A、B同时出发,其中M、N均向右运动,速度分别为2个单位长度/秒,7个单位长度/秒,点P向左运动,速度为8个单位长度/秒,设它们运动时间为t秒,问当t为何值时,点M、N之间的距离等于P、M之间的距离;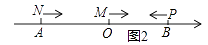
(3)如图3,将(2)中的三动点M、N、P的运动方向改为与原来相反的方向,其余条件不变,设Q为线段MN的中点,R为线段OP的中点,求22RQ﹣28RO﹣5PN的值.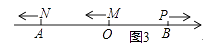
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个圆锥的底面半径为4cm,将侧面展开后所得扇形的半径为5cm,那么这个圆锥的侧面积等于______cm2(结果保留π).
相关试题

