【题目】如图,在平面直角坐标系中,O是坐标原点,点A的坐标为(4,0),点B的坐标为(0,b)(b>0),点P是直线AB上位于第二象限内的一个动点,过点P作PC⊥x轴于点C,记点P关于y轴的对称点为Q,设点P的横坐标为a.
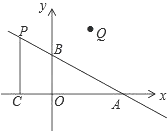
(1)当b=3时,
①求直线AB的解析式;
②若QO=QA,求P点的坐标.
(2)是否同时存在a、b,使得△QAC是等腰直角三角形?若存在,求出所有满足条件的a、b的值;若不存在,请说明理由.
参考答案:
【答案】(1)y=-![]() x+3;P坐标得P(-2,
x+3;P坐标得P(-2,![]() );(2)a=-4,b=4或a=-
);(2)a=-4,b=4或a=-![]() ,b=2.
,b=2.
【解析】
试题分析:(1)①由题意确定出B坐标,设直线AB解析式为y=kx+b,把A与B坐标代入求出k与b的值,即可求出AB解析式;②由AQ=QO以及OA的长,确定出Q横坐标,根据P与Q关于y轴对称,得出P横坐标,代入直线AB解析式求出纵坐标,即可确定出P坐标;
(2)同时存在a、b,使得△QAC是等腰直角三角形,分两种情况考虑:①若∠QAC=90°;②若∠AQC=90°,分别求出a与b的值即可.
试题解析:(1)①由A(4,0),B(0,3),
设直线AB解析式为y=kx+b,
把A与B坐标代入得:![]() ,
,
解得:k=-![]() ,b=3,
,b=3,
则直线AB解析式为y=-![]() x+3;
x+3;
②∵QA=QO,OA=4,
∴xQ=2,
∵点P关于y轴的对称点为Q,
∴xP=-2,
代入直线AP解析式得-![]() ×(-2)+3=
×(-2)+3=![]() ,
,
则P坐标得P(-2,![]() );
);
(2)①若∠QAC=90°,如图1所示,
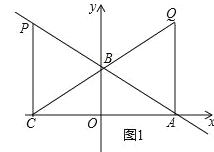
∴xQ=4,
∴a=xP=-4,
∴AC=AQ=8,即P(-4,8),
∴直线AP解析式为y=-x+4,
∴a=-4,b=4;
②若∠AQC=90°,如图2所示,
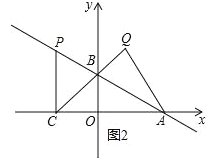
则AC=4-a=2CH=-4a,
∴a=-![]() ,
,
∴xP=-![]() ,yP=yq=
,yP=yq=![]() ,即P(-
,即P(-![]() ,
,![]() ),
),
∴直线AP解析式为y=-![]() x+2,
x+2,
∴a=-![]() ,b=2,
,b=2,
综上所示,a=-4,b=4或a=-![]() ,b=2.
,b=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2﹣6x+k=0.
(1)当它有两个实数根时,求k的范围;
(2)当k=﹣11时,假设方程两根是x1,x2,求x12+x22+8的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简,求值
(1)5x2y+{xy﹣[5x2y﹣(7xy2+
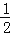 xy)]﹣(4x2y+xy)}﹣7xy2,其中x=﹣
xy)]﹣(4x2y+xy)}﹣7xy2,其中x=﹣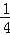 ,y=﹣16.
,y=﹣16.(2)A=4x2﹣2xy+4y2,B=3x2﹣6xy+3y2,且|x|=3,y2=16,|x+y|=1,求4A+[(2A﹣B)﹣3(A+B)]的值.
(3)如果m﹣3n+4=0,求:(m﹣3n)2+7m3﹣3(2m3n﹣m2n﹣1)+3(m3+2m3n﹣m2n+n)﹣m﹣10m3的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,AB=AC=2,O为AC中点,若点D在直线BC上运动,连接OE,则在点D运动过程中,线段OE的最小值是为( )

A.
 B.
B. C.1 D.
C.1 D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地.设先发车辆行驶的时间为x h,两车之间的距离为y km.当两车均到达各自终点时,运动停止.如图是y与x之间函数关系的部分图象.
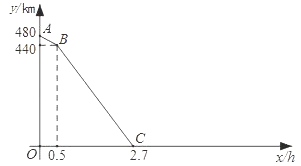
(1)由图象知,慢车的速度为 km/h,快车的速度为 km/h;
(2)请在图中补全函数图象;
(3)求当x为多少时,两车之间的距离为300km.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某草莓种植农户喜获丰收,共收获草莓2000kg.经市场调查,可采用批发、零售两种销售方式,这两种销售方式每kg草莓的利润如下表:
销售方式
批发
零售
利润(元/kg)
6
12
设按计划全部售出后的总利润为y元,其中批发量为xkg.
(1)求y与x之间的函数关系式;
(2)若零售量不超过批发量的4倍,求该农户按计划全部售完后获得的最大利润.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OA的方向是北偏东15°,OB的方向是西偏北50度.
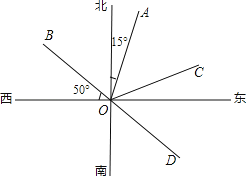
(1)若∠AOC=∠AOB,则OC的方向是 ;
(2)OD是OB的反向延长线,OD的方向是 ;
(3)∠BOD可看作是OB绕点O逆时针方向至OD,作∠BOD的平分线OE,OE的方向是 ;
(4)在(1)、(2)、(3)的条件下,∠COE= .
相关试题

