【题目】如图,在矩形ABCD中,点F在边BC上,且AF=AD,过点D作DE⊥AF,垂足为点E。
(1)求证:DE=AB;
(2)以D为圆心,DE为半径作圆弧交AD于点G,若BF=FC=1,试求![]() 的长。
的长。

参考答案:
【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)根据矩形的性质得出∠B=90°,AD=BC,AD∥BC,求出∠DAE=∠AFB,∠AED=90°=∠B,根据AAS推出△ABF≌△DEA即可;
(2)根据勾股定理求出AB,解直角三角形求出∠BAF,根据全等三角形的性质得出DE=DG=AB=![]() ,∠GDE=∠BAF=30°,根据弧长公式求得求出即可.
,∠GDE=∠BAF=30°,根据弧长公式求得求出即可.
试题解析:(1)在△ABF和△DEA中,
∠AFB=∠DAE
∠B=∠DEA
AF=AD,
∴△ABF≌△DEA ∴DE=AB.
(2)∵BC=AD,AD=AF,
∴BC=AF.
∵BF=1,∠ABF=90°,
∴由勾股定理得:AB=![]()
∴∠BAF=30°.
∵△ABF≌△DEA,
∴∠GDE=∠BAF=30°,DE=AB=DG=![]()
∴ ![]() 的长为
的长为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一条不完整的数轴上从左到右有点A,B,D,C,其中AB=2,BD=3,DC=1,如图所示,设点A,B,D,C所对应数的和是p.
(1)若以B为原点.写出点A,D,C所对应的数,并计算p的值;
(2)若原点O在图中数轴上点C的右边,且CO=x,p=﹣71,求x的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系xoy中,点P的坐标为(m+1,m-1).
(1)试判断点P是否在一次函数y=x-2的图象上,并说明理由;
(2)如图,一次函数y= -
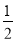 x+3的图象与x轴、y轴分别相交于点A、B,若点P在△AOB的内部,求m的取值范围.
x+3的图象与x轴、y轴分别相交于点A、B,若点P在△AOB的内部,求m的取值范围.(3)若点P在直线AB上,已知点R(
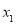 ,
,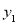 ),S(
),S(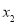 ,
,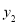 )在直线y=kx+b上,b>2,
)在直线y=kx+b上,b>2,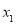 +
+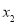 =mb,
=mb, 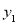 +
+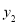 =kb+4若
=kb+4若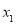 >
>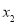 ,判断
,判断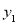 与
与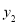 的大小关系
的大小关系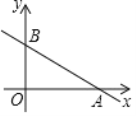
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明随机调查了若干市民租用公共自行车的骑车时间t(单位:分),将获得的数据分成四组,绘制了如下统计图。请根据图中信息,解答下列问题:
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/12/1922393511583744/1923977001213952/STEM/d5900c7cb9b84a9a89aefef7d82bcf93.png]
(1)这次被调查的总人数是多少?
(2)试求表示A组的扇形圆心角的度数,并补全条形统计图;
(3)如果骑自行车的平均速度为12km/h,请估算,在租用公共自行车的市民中,骑车路程不超过6km的人数所占的百分比。
-
科目: 来源: 题型:
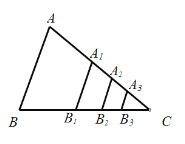
查看答案和解析>>【题目】如图,△ABC的面积为1,分别取AC、BC两边的中点A1、B1,则四边形A1ABB1的面积为
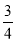 ,再分别取A1C、B1C的中点A2、B2,取A2C、B2C的中点A3、B3,依次取下去…利用这一图形,能直观地计算出
,再分别取A1C、B1C的中点A2、B2,取A2C、B2C的中点A3、B3,依次取下去…利用这一图形,能直观地计算出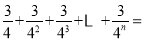 ( )
( )
A. 1B.
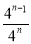 C.
C. 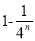 D.
D. 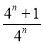
-
科目: 来源: 题型:
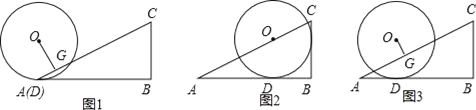
查看答案和解析>>【题目】如图,△ABC中,∠B=90°,tan∠BAC=
 ,半径为2的⊙O从点A开始(图1),沿AB向右滚动,滚动时始终与AB相切(切点为D);当圆心O落在AC上时滚动停止,此时⊙O与BC相切于点E(图2).作OG⊥AC于点G.
,半径为2的⊙O从点A开始(图1),沿AB向右滚动,滚动时始终与AB相切(切点为D);当圆心O落在AC上时滚动停止,此时⊙O与BC相切于点E(图2).作OG⊥AC于点G.(1)利用图2,求cos∠BAC的值;
(2)当点D与点A重合时(如图1),求OG;
(3)如图3,在⊙O滚动过程中,设AD=x,请用含x的代数式表示OG,并写出x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数填入相应的横线上:
-2,2π,
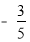 ,0,-3.7,
,0,-3.7,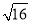 ,0.35,
,0.35,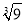
整数:______________________; 正有理数:__________________;
无理数:____________________; 负分数:_____________________.
相关试题

