【题目】如图,BF为⊙O的直径,直线AC交⊙O于A,B两点,点D在⊙O上,BD平分∠OBC,DE⊥AC于点E.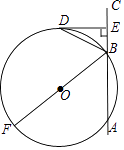
(1)求证:直线DE是⊙O的切线;
(2)若 BF=10,sin∠BDE= ![]() ,求DE的长.
,求DE的长.
参考答案:
【答案】
(1)证明:如图所示,连接OD,
∵OD=OB,
∴∠ODB=∠OBD,
∵BD平分∠OBC,
∴∠OBD=∠DBE,
∴∠ODB=∠DBE,
∴OD∥AC,
∵DE⊥AC,
∴OD⊥DE,
∵OD是⊙O的半径,
∴直线DE是⊙O的切线
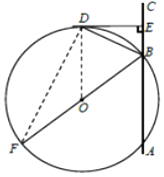
(2)解:如图,连接DF,
∵BF是⊙O的直径,
∴∠FDB=90°,
∴∠F+∠OBD=90°,
∵∠OBD=∠DBE,∠BDE+∠DBE=90°,
∴∠F=∠BDE,
在Rt△BDF中, ![]() =sinF=sin∠BDE=
=sinF=sin∠BDE= ![]() ,
,
∴BD=10× ![]() =2
=2 ![]() ,
,
∴在Rt△BDE中,sin∠BDE= ![]() =
= ![]() ,
,
∴BE=2 ![]() ×
× ![]() =2,
=2,
∴在Rt△BDE中,DE= ![]() =
= ![]() =4.
=4.

【解析】(1)先连接OD,根据∠ODB=∠DBE,即可得到OD∥AC,再根据DE⊥AC,可得OD⊥DE,进而得出直线DE是⊙O的切线;(2)先连接DF,根据题意得到∠F=∠BDE,在Rt△BDF中,根据 ![]() =sinF=sin∠BDE=
=sinF=sin∠BDE= ![]() ,可得BD=2
,可得BD=2 ![]() ,在Rt△BDE中,根据sin∠BDE=
,在Rt△BDE中,根据sin∠BDE= ![]() =
= ![]() ,可得BE=2,最后依据勾股定理即可得到DE的长.
,可得BE=2,最后依据勾股定理即可得到DE的长.
【考点精析】通过灵活运用解直角三角形,掌握解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 画射线
画射线 ,射线
,射线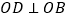 ,试写出
,试写出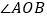 和
和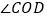 的数量关系,并说明理由.
的数量关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.哥哥的身高比弟弟高是必然事件
B.今年的12月1日有雨是不确定事件
C.随机掷一枚均匀的硬币两次,都是正面朝上是不可能事件
D.“彩票中奖的概率为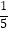 ”表示买5张彩票肯定会中奖
”表示买5张彩票肯定会中奖 -
科目: 来源: 题型:
查看答案和解析>>【题目】
 、
、 两地相距
两地相距 ,甲、乙两车分别沿同一条路线从
,甲、乙两车分别沿同一条路线从 地出发驶往
地出发驶往 地,已知甲车的速度为
地,已知甲车的速度为 ,乙车的速度为
,乙车的速度为 ,甲车先出发
,甲车先出发 后乙车再出发,乙车到达
后乙车再出发,乙车到达 地后再原地等甲车.
地后再原地等甲车.(1)求乙车出发多长时间追上甲车?
(2)求乙车出发多长时间与甲车相距
 ?
? -
科目: 来源: 题型:
查看答案和解析>>【题目】若点A(﹣2,y1),B(1,y2),C(2,y3)是抛物线y=﹣(x+1)2+a上的三点,则y1 , y2 , y3的大小关系为( )
A.y3>y1>y2
B.y1>y3>y2
C.y3>y2>y1
D.y1>y2>y3 -
科目: 来源: 题型:
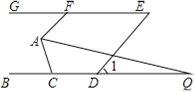
查看答案和解析>>【题目】如图,已知BC∥GE,AF∥DE,点D在直线BC上,点F在直线GE上,且∠1=50°.
(1)求∠AFG的度数;
(2)若AQ平分∠FAC,交直线BC于点Q,且∠Q=18°,则∠ACB的度数为______°.(直接写出答案)
-
科目: 来源: 题型:
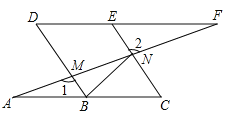
查看答案和解析>>【题目】如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠A=∠F,∠1=∠2.
(1)求证:四边形BCED是平行四边形;
(2)已知DE=2,连接BN,若BN平分∠DBC,求CN的长.
相关试题

