【题目】在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,且∠B、∠E都是锐角,∠C<90°,若∠B满足条件:______________,则△ABC≌△DEF.
参考答案:
【答案】∠B≥∠A.
【解析】
虽然题目中∠B为锐角,但是需要对∠B进行分类探究会理解更深入:可按“∠B是直角、钝角、锐角”三种情况进行,最后得出∠B、∠E都是锐角时两三角形全等的条件.
解:需分三种情况讨论:
第一种情况:当∠B是直角时:
如图①,在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E=90°,可知:△ABC与△DEF一定全等,依据的判定方法是HL;
第二种情况:当∠B是钝角时:如图②,过点C作CG⊥AB交AB的延长线于G,过点F作DH⊥DE交DE的延长线于H.
∵∠B=∠E,且∠B、∠E都是钝角.
∴180°-∠B=180°-∠E,
即∠CBG=∠FEH.
在△CBG和△FEH中,

∴△CBG≌△FEH(AAS),
∴CG=FH,
在Rt△ACG和Rt△DFH中,
![]()
∴Rt△ACG≌Rt△DFH(HL),
∴∠A=∠D,
在△ABC和△DEF中,

∴△ABC≌△DEF(AAS);
第三种情况:当∠B是锐角时:
在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,且∠B、∠E都是锐角,小明在△ABC中(如图③)以点C为圆心,以AC长为半径画弧交AB于点D,假设E与B重合,F与C重合,得到△DEF与△ABC符号已知条件,但是△AEF与△ABC一定不全等,
所以有两边和其中一边的对角对应相等的两个三角形不一定全等;
由图③可知,∠A=∠CDA=∠B+∠BCD,
∴∠A>∠B,
∴当∠B≥∠A时,△ABC就唯一确定了,
则△ABC≌△DEF.
故答案为:∠B≥∠A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,将坐标原点O沿x轴向左平移2个单位长度得到点A,过点A作y轴的平行线交反比例函数y=
 的图象于点B,AB=
的图象于点B,AB= .
.(1)求反比例函数的解析式;
(2)若P(x1,y1)、Q(x2,y2)是该反比例函数图象上的两点,且x1<x2时,y1>y2,指出点P、Q各位于哪个象限?并简要说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC三个内角的平分线交于点O,点D在CA的延长线上,且DC=BC,AD=AO,若∠BAC=80°,则∠BCA的度数为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】函数y1=x(x≥0),y2=
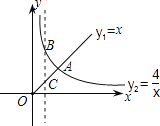
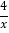 (x>0)的图象如图6-Z-6所示,则下列结论:
(x>0)的图象如图6-Z-6所示,则下列结论:①两函数图象的交点A的坐标为(2,2);
②当x>2时,y1>y2;
③当x=1时,BC=3;
④当x逐渐增大时,y1随着x的增大而增大,y2随着x的增大而减小.
其中正确结论的序号是________.
-
科目: 来源: 题型:
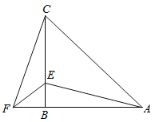
查看答案和解析>>【题目】如图,在△ABC中,AB=CB,∠BAC=∠BCA=45°,F为AB延长线上一点,点E在BC上,且BE=BF.∠CAE=30°,求∠ACF的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材
有依次排列的
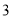 个数:
个数: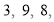 对任意相邻的两个数,都用右边的数减去左边的数,所得之差写在这两个数之间,可产生一个新数串:
对任意相邻的两个数,都用右边的数减去左边的数,所得之差写在这两个数之间,可产生一个新数串: 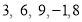 这称为第一次操作;第二次同样的操作后也可产生一个新数串:
这称为第一次操作;第二次同样的操作后也可产生一个新数串: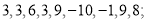 继续依次操作下去.问
继续依次操作下去.问 有依次排开的
有依次排开的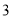 个数:
个数: 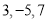 ,第一次操作后,增加的所有新数之和是多少?
,第一次操作后,增加的所有新数之和是多少? 在
在 的前提下,经过第二次操作后所得的新数串比第一次操作后所得的数串增加的所有新数之和是多少?
的前提下,经过第二次操作后所得的新数串比第一次操作后所得的数串增加的所有新数之和是多少?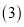 猜想:有依次排开的
猜想:有依次排开的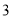 个数,
个数,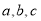 第一百次操作后得到的新数串比第九十九次操作后所得的数串增加的所有新数之和是多少?
第一百次操作后得到的新数串比第九十九次操作后所得的数串增加的所有新数之和是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF,
(1)求证:AD平分∠BAC;(2)已知AC=20, BE=4,求AB的长.

相关试题

