搜索
【题目】已知A，B为多项式，B=x+1，计算A+B时,某学生把A+B看成A÷B，结果得2x2-2x+1，请你求出A+B的正确答案．
参考答案：
【答案】2x3+2
【解析】
根据题意，已知B=x+1，某学生把A+B看成A÷B即A÷B=A÷（x+1）=2x2-2x+1，根据被除数=商×除数可先求出A，进而计算A+B．
解：根据题意得，A÷B=A÷（x+1）=2x2-2x+1，
∴A=（x+1）×（2x2-2x+1）=2x3-x+1，
∴A+B=2x3-x+1+x+1=2x3+2，
即A+B的正确答案为2x3+2．
-
科目： 来源： 题型：
查看答案和解析>>【题目】列式表示比a的6倍小3的数与比a的4倍大1的数，计算这两个数的和．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在四边形ABCD中，∠DAB=∠ABC=90
,AD∥BC,AB=BC,E是AB的中点，CE⊥BD.(1)求证：BE=AD；
(2)求证：AC是线段ED的垂直平分线;
(3)△DBC是等腰三角形吗？并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在边长为1的正方形网格中建立平面直角坐标系，已知△ABC三个顶点分别为A（﹣1，2）、B（2，1）、C（4，5）．
（1）画出△ABC关于x对称的△A1B1C1；
（2）以原点O为位似中心，在x轴的上方画出△A2B2C2，使△A2B2C2与△ABC位似，且位似比为2，并求出△A2B2C2的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某学校初一年级参加社会实践课，报名第一门课的有x人，第二门课的人数比第一门课的
少10人，现在需要从报名第二门课的人中调出10人学习第一门课，那么：（1）报两门课的共有多少人？
（2）调动后，报名第一门课的人数为 人，第二门课人数为 人．
（3）调动后，报名第一门课比报名第二门课多多少人？计算出代数式后，请选择一个你觉得合适的x的值代入，并求出具体的人数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下面材料并解决有关问题：
我们知道：|x|=
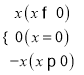．现在我们可以用这一结论来化简含有绝对值的代数式，现在我们可以用这一结论来化简含有绝对值的代数式，如化简代数式|x+1|+|x﹣2|时，可令x+1=0和x﹣2=0，分别求得x=﹣1，x=2（称﹣1，2分别为|x+1|与|x﹣2|的零点值）．在实数范围内，零点值x=﹣1和，x=2可将全体实数分成不重复且不遗漏的如下3种情况：①x＜﹣1；②﹣1≤x＜2；③x≥2．
从而化简代数式|x+1|+|x﹣2|可分以下3种情况：
①当x＜﹣1时，原式=﹣（x+1）﹣（x﹣2）=﹣2x+1；
②当﹣1≤x＜2时，原式=x+1﹣（x﹣2）=3；
③当x≥2时，原式=x+1+x﹣2=2x﹣1．综上讨论，原式=
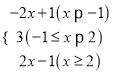．通过以上阅读，请你解决以下问题：
（1）化简代数式|x+2|+|x﹣4|．
（2）求|x﹣1|﹣4|x+1|的最大值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某高速铁路工程指挥部，要对某路段工程进行招标，接到了甲、乙两个工程队的投标书．从投标书中得知：甲队单独完成这项工程所需天数是乙队单独完成这项工程所需天数的
：若由甲队先做20天，剩下的工程再由甲、乙两队合作60天完成．(1)求甲、乙两队单独完成这项工程各需多少天？
(2)已知甲队每天的施工费用为8.6万元，乙队每天的施工费用为5.4万元，工程预算的施工费用为1000万元．若在甲、乙工程队工作效率不变的情况下使施工时间最短，问拟安排预算的施工费用是否够用？若不够用，需追加预算多少万元？
相关试题
