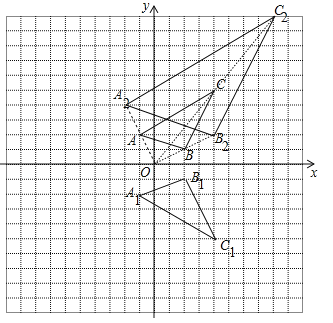
【题目】如图,在边长为1的正方形网格中建立平面直角坐标系,已知△ABC三个顶点分别为A(﹣1,2)、B(2,1)、C(4,5).
(1)画出△ABC关于x对称的△A1B1C1;
(2)以原点O为位似中心,在x轴的上方画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2,并求出△A2B2C2的面积.

参考答案:
【答案】(1)作图见解析;(2)作图见解析,28.
【解析】试题分析:(1)画出A、B、C关于x轴的对称点A1、B1、C1即可解决问题;
(2)连接OB延长OB到B2,使得OB=BB2,同法可得A2、C2,△A2B2C2就是所求三角形;
试题解析:解:(1)如图所示,△A1B1C1就是所求三角形;
(2)如图所示,△A2B2C2就是所求三角形.
如图,分别过点A2、C2作y轴的平行线,过点B2作x轴的平行线,交点分别为E、F,∵A(﹣1,2),B(2,1),C(4,5),△A2B2C2与△ABC位似,且位似比为2,∴A2(﹣2,4),B2(4,2),C2(8,10),∴![]() =8×10﹣
=8×10﹣![]() ×6×2﹣
×6×2﹣![]() ×4×8﹣
×4×8﹣![]() ×6×10=28.
×6×10=28.
-
科目: 来源: 题型:
查看答案和解析>>【题目】单项式﹣4x2的系数是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】列式表示比a的6倍小3的数与比a的4倍大1的数,计算这两个数的和.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠DAB=∠ABC=90
 ,AD∥BC,AB=BC,E是AB的中点,CE⊥BD.
,AD∥BC,AB=BC,E是AB的中点,CE⊥BD.(1)求证:BE=AD;
(2)求证:AC是线段ED的垂直平分线;
(3)△DBC是等腰三角形吗?并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A,B为多项式,B=x+1,计算A+B时,某学生把A+B看成A÷B,结果得2x2-2x+1,请你求出A+B的正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校初一年级参加社会实践课,报名第一门课的有x人,第二门课的人数比第一门课的
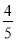 少10人,现在需要从报名第二门课的人中调出10人学习第一门课,那么:
少10人,现在需要从报名第二门课的人中调出10人学习第一门课,那么:(1)报两门课的共有多少人?
(2)调动后,报名第一门课的人数为 人,第二门课人数为 人.
(3)调动后,报名第一门课比报名第二门课多多少人?计算出代数式后,请选择一个你觉得合适的x的值代入,并求出具体的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料并解决有关问题:
我们知道:|x|=
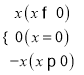 .现在我们可以用这一结论来化简含有绝对值的代数式,现在我们可以用这一结论来化简含有绝对值的代数式,如化简代数式|x+1|+|x﹣2|时,可令x+1=0和x﹣2=0,分别求得x=﹣1,x=2(称﹣1,2分别为|x+1|与|x﹣2|的零点值).在实数范围内,零点值x=﹣1和,x=2可将全体实数分成不重复且不遗漏的如下3种情况:
.现在我们可以用这一结论来化简含有绝对值的代数式,现在我们可以用这一结论来化简含有绝对值的代数式,如化简代数式|x+1|+|x﹣2|时,可令x+1=0和x﹣2=0,分别求得x=﹣1,x=2(称﹣1,2分别为|x+1|与|x﹣2|的零点值).在实数范围内,零点值x=﹣1和,x=2可将全体实数分成不重复且不遗漏的如下3种情况:①x<﹣1;②﹣1≤x<2;③x≥2.
从而化简代数式|x+1|+|x﹣2|可分以下3种情况:
①当x<﹣1时,原式=﹣(x+1)﹣(x﹣2)=﹣2x+1;
②当﹣1≤x<2时,原式=x+1﹣(x﹣2)=3;
③当x≥2时,原式=x+1+x﹣2=2x﹣1.综上讨论,原式=
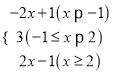 .
.通过以上阅读,请你解决以下问题:
(1)化简代数式|x+2|+|x﹣4|.
(2)求|x﹣1|﹣4|x+1|的最大值.
相关试题

