【题目】如图,四边形ABCD内接于⊙O,点E在对角线AC上,EC=BC=DC.

(1)若∠CBD=40°,求∠BAD的度数;
(2)求证:∠1=∠2.
参考答案:
【答案】(1)80°;(2)参见解析.
【解析】
试题分析:(1)根据BC=DC,∠CBD=40°,先算出∠CDB的度数,再根据同弧所对的圆周角相等,求出∠BAC和∠CAD的度数,从而求得∠BAD的度数;(2)由EC=BC得出∠CEB=∠CBE,再根据∠CEB=∠2+∠BAE,∠CBE=∠1+∠CBD,得出∠2+∠BAE=∠1+∠CBD,因为∠BAE=∠BDC =∠CBD,所以可得出∠1=∠2.
试题解析:(1)∵BC=CD, ∴∠CBD=∠CDB=40°,∴∠BAC=∠CDB=40°,∠CAD=∠CBD=40° ∴∠BAD=∠BAC+∠CAD=40°+40°=80°;(2)由题意得:EC=BC, ∴∠CEB=∠CBE,而由图可知:∠CEB=∠2+∠BAE,∠CBE=∠1+∠CBD,∴∠2+∠BAE=∠1+∠CBD,又∵∠BAE=∠BDC =∠CBD,∴∠1=∠2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种零件,标明要求是φ20±0.02 mm(φ表示直径,单位:毫米),经检查,一个零件的直径是19.9 mm,该零件 (填“合格”或“不合格”).
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个长方形在平面直角坐标系中三个顶点的坐标为(-1,-2),(3,-2),(3,1),则第四个顶点的坐标为( )
A. (-1,1)B. (1,-1)C. (-1,2)D. (1,1)
-
科目: 来源: 题型:
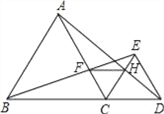
查看答案和解析>>【题目】如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F, AD交CE于H.
(1)求证:∠CAD=∠CBE
(2)求证:FH∥BD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】比较大小:﹣|﹣0.8|﹣(﹣0.8)(填“>”或“<”或“=”).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中
中 ,
,  于点
于点 ,
,  于点
于点 ,
,  为
为 边的中点,连接
边的中点,连接 、
、 ,则下列结论:①
,则下列结论:① ;②
;② 为等边三角形.下面判断正确是( )
为等边三角形.下面判断正确是( )
A. ①正确 B. ②正确
C. ①②都正确 D. ①②都不正确
-
科目: 来源: 题型:
查看答案和解析>>【题目】设点M(1,2)关于原点的对称点为M′,则M′的坐标为 .
相关试题

