【题目】阅读下面材料:
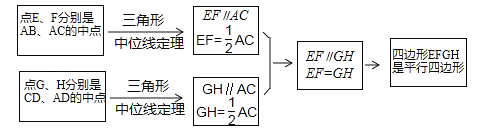
在数学课上,老师请同学思考如下问题:如图1,我们把一个四边形ABCD的四边中点E,F,G,H依次连接起来得到的四边形EFGH是平行四边形吗?
小敏在思考问题是,有如下思路:连接AC.
结合小敏的思路作答
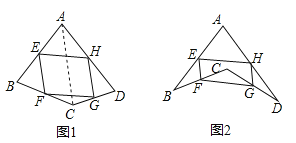
(1)若只改变图1中四边形ABCD的形状(如图2),则四边形EFGH还是平行四边形吗?说明理由;参考小敏思考问题方法解决一下问题:
(2)如图2,在(1)的条件下,若连接AC,BD.
①当AC与BD满足什么条件时,四边形EFGH是菱形,写出结论并证明;
②当AC与BD满足什么条件时,四边形EFGH是矩形,直接写出结论.
参考答案:
【答案】(1)是平行四边形;(2)①AC=BD;②AC⊥BD.
【解析】
试题分析:(1)如图2,连接AC,根据三角形中位线的性质得到EF∥AC,EF=![]() AC,然后根据平行四边形判定定理即可得到结论;
AC,然后根据平行四边形判定定理即可得到结论;
(2)①由(1)知,四边形EFGH是平行四边形,且FG=![]() BD,HG=
BD,HG=![]() AC,于是得到当AC=BD时,FG=HG,即可得到结论;
AC,于是得到当AC=BD时,FG=HG,即可得到结论;
②根据平行线的性质得到GH⊥BD,GH⊥GF,于是得到∠HGF=90°,根据矩形的判定定理即可得到结论.
试题解析:(1)是平行四边形.证明如下:
如图2,连接AC,∵E是AB的中点,F是BC的中点,∴EF∥AC,EF=![]() AC,同理HG∥AC,HG=
AC,同理HG∥AC,HG=![]() AC,综上可得:EF∥HG,EF=HG,故四边形EFGH是平行四边形;
AC,综上可得:EF∥HG,EF=HG,故四边形EFGH是平行四边形;
(2)①AC=BD.
理由如下:
由(1)知,四边形EFGH是平行四边形,且FG=![]() BD,HG=
BD,HG=![]() AC,∴当AC=BD时,FG=HG,∴平行四边形EFGH是菱形;
AC,∴当AC=BD时,FG=HG,∴平行四边形EFGH是菱形;
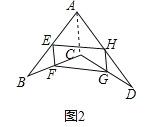
②当AC⊥BD时,四边形EFGH为矩形;理由如下:
同(2)得:四边形EFGH是平行四边形,∵AC⊥BD,GH∥AC,∴GH⊥BD,∵GF∥BD,∴GH⊥GF,∴∠HGF=90°,∴四边形EFGH为矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上有A、B、C这三个点,请回答:

(1)A、B、C这三个点表示的数各是多少?
(2)A、B两点间的距离是多少?A、C两点间的距离是多少?
(3)若将点A向右移动4个单位后,则A、B、C这三个点所表示的数谁最大?最大的数比最小的数大多少?
(4)应怎样移动点B的位置,使点B到点A和点C的距离相等?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,点F在边BC上,且AF=AD,过点D作DE⊥AF,垂足为点E
(1)求证:DE=AB;
(2)以A为圆心,AB长为半径作圆弧交AF于点G,若BF=FC=1,求扇形ABG的面积.(结果保留π)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=AD,那添加下列一个条件后,仍无法判定△ABC≌△ADC的是 ( )
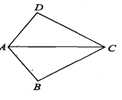
A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列多边形一定相似的是( )
A.两个平行四边形
B.两个菱形
C.两个矩形
D.两个正方形 -
科目: 来源: 题型:
查看答案和解析>>【题目】从A地途径B地、C地,终点E地的长途汽车上原有乘客(6x+2y)人,在B地停靠时,上来(2x﹣y)人,在C地停靠时,上来了(2x+3y)人,又下去了(5x﹣2y)人.
(1)途中两次共上车多少人?
(2)到终点站E地时,车上共有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若方程 x2+px+3=0 的一个根是﹣3,则它的另一个根是( )
A. ﹣1B. 0C. 1D. 2
相关试题

