搜索
【题目】字母m、n分别表示一个有理数，且m≠n．现规定min{m，n}表示m、n中较小的数，例如：min{3，﹣1}＝﹣1，min{﹣1，0}＝﹣1．据此解决下列问题：
（1）min{﹣
，﹣
}＝ ．
（2）若min{
，2）＝﹣1，求x的值；
（3）若min{2x﹣5，x+3}＝﹣2，求x的值．
参考答案：
【答案】（1）﹣
；（2）x＝﹣1；（3）x＝1.5
【解析】
(1)根据新定义代入即可.
(2)根据新定义代入,再解出方程即可
(3)根据新定义代入,解出方程,讨论结果.
解：（1）根据题中的新定义得：min{﹣，﹣
}＝﹣；
故答案为：﹣；
（2）由2＞﹣1，得到
＝﹣1，
解得：x＝﹣1；
（3）若2x﹣5＝﹣2，解得：x＝1.5，此时x+3＝4.5＞﹣2，满足题意；
若x+3＝﹣2，解得：x＝﹣5，此时2x﹣5＝﹣15＜﹣2，不符合题意，
综上，x＝1.5．
-
科目： 来源： 题型：
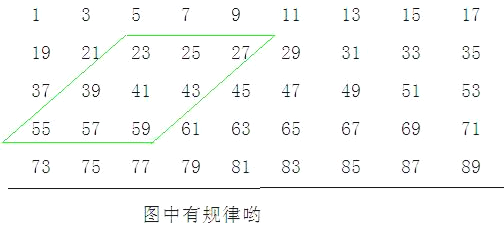
查看答案和解析>>【题目】下图的数阵是由全体奇数排成：
（1）图中平行四边形框内的九个数之和与中间的数有什么关系？
（2）在数阵图中任意作一类似（1）中的平行四边形框，这九个数之和还有这种规律吗？请说出理由；
（3）这九个数之和能等于1998吗？2005，1017呢？若能，请写出这九个数中最小的一个；若不能，请说出理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下列材料： 1×2=
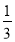(1×2×3-0×1×2)，2×3= 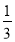(2×3×4-1×2×3)，3×4= 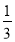(3×4×5- 2×3×4)，由以上三个等式左、右两边分别相加，可得：
1×2+2×3+3×4=
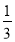×3×4×5=20 读完以上材料，请你计算下列各题(写出过程)：
(1)1×2+2×3+3×4+…+10×11= ；
(2)1×2+2×3+3×4+…+n×(n+1)= .
-
科目： 来源： 题型：
查看答案和解析>>【题目】（规律探索）如图所示的是由相同的小正方形组成的图形，每个图形的小正方形个数为Sn，n是正整数．观察下列图形与等式之间的关系．
第一组：
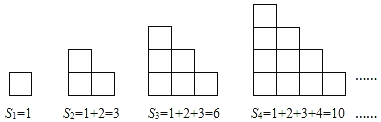
第二组：
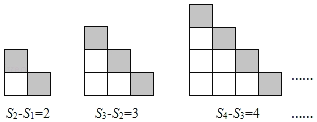
第三组：
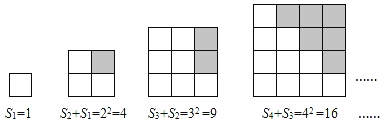
（规律归纳）
（1）S7﹣S6＝ ；Sn﹣Sn﹣1＝ ．
（2）S7+S6＝ ；Sn+Sn﹣1＝ ．
（规律应用）
（3）计算
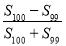的结果为 ． -
科目： 来源： 题型：
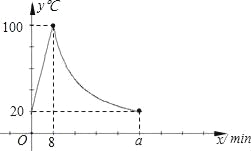
查看答案和解析>>【题目】某小学为每个班级配备了一种可以加热的饮水机，该饮水机的工作程序是：放满水后，接通电源，则自动开始加热，每分钟水温上升10℃，待加热到100℃，饮水机自动停止加热，水温开始下降，水温y（℃）和通电时间x（min）成反比例关系，直至水温降至室温，饮水机再次自动加热，重复上述过程．设某天水温和室温为20℃，接通电源后，水温和时间的关系如下图所示，回答下列问题：
（1）分别求出当0≤x≤8和8＜x≤a时，y和x之间的关系式；
（2）求出图中a的值；
（3）下表是该小学的作息时间，若同学们希望在上午第一节下课8：20时能喝到不超过40℃的开水，已知第一节下课前无人接水，请直接写出生活委员应该在什么时间或时间段接通饮水机电源．（不可以用上课时间接通饮水机电源）
时间
节次
上
午
7：20
到校
7：45～8：20
第一节
8：30～9：05
第二节
…
…
-
科目： 来源： 题型：
查看答案和解析>>【题目】某商场准备进一批两种不同型号的衣服，已知购进A种型号衣服9件，B种型号衣服10件，则共需1810元；若购进A种型号衣服12件，B种型号衣服8件，共需1880元；已知销售一件A型号衣服可获利18元，销售一件B型号衣服可获利30元，要使在这次销售中获利不少于699元，且A型号衣服不多于28件．
（1）求A、B型号衣服进价各是多少元？
（2）若已知购进A型号衣服是B型号衣服的2倍还多4件，则商店在这次进货中可有几种方案并简述购货方案．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在Rt△ABC中，∠C=90°，以AC为直径作⊙O，交AB于D，过点O作OE∥AB，交BC于E．
（1）求证：ED为⊙O的切线；
（2）如果⊙O的半径为
，ED=2，延长EO交⊙O于F，连接DF、AF，求△ADF的面积．
【答案】（1）证明见解析；（2）
【解析】试题分析：（1）首先连接OD，由OE∥AB，根据平行线与等腰三角形的性质，易证得
≌
即可得
，则可证得
为
的切线；
（2）连接CD，根据直径所对的圆周角是直角，即可得
利用勾股定理即可求得
的长，又由OE∥AB，证得
根据相似三角形的对应边成比例，即可求得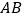
的长，然后利用三角函数的知识，求得
与
的长，然后利用S△ADF=S梯形ABEF-S梯形DBEF求得答案．试题解析：(1)证明：连接OD，
∵OE∥AB，
∴∠COE=∠CAD，∠EOD=∠ODA，
∵OA=OD,
∴∠OAD=∠ODA，
∴∠COE=∠DOE，
在△COE和△DOE中，
∴△COE≌△DOE(SAS)，
∴ED⊥OD，
∴ED是
的切线；(2)连接CD，交OE于M，
在Rt△ODE中，
∵OD=32，DE=2，
∵OE∥AB，
∴△COE∽△CAB，
∴AB=5，∵AC是直径，
∵EF∥AB，
∴S△ADF=S梯形ABEFS梯形DBEF
∴△ADF的面积为
【题型】解答题
【结束】
25【题目】【题目】已知，抛物线y=ax2+ax+b（a≠0）与直线y=2x+m有一个公共点M（1，0），且a＜b．
（1）求b与a的关系式和抛物线的顶点D坐标（用a的代数式表示）；
（2）直线与抛物线的另外一个交点记为N，求△DMN的面积与a的关系式；
（3）a=﹣1时，直线y=﹣2x与抛物线在第二象限交于点G，点G、H关于原点对称，现将线段GH沿y轴向上平移t个单位（t＞0），若线段GH与抛物线有两个不同的公共点，试求t的取值范围．
相关试题
