【题目】如图,反比例函数y= ![]() (x<0)的图象经过点A(﹣1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则t的值是( )
(x<0)的图象经过点A(﹣1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则t的值是( )
A.![]()
B.![]()
C.![]()
D.![]()
参考答案:
【答案】A
【解析】解:如图,
∵点A坐标为(﹣1,1),
∴k=﹣1×1=﹣1,
∴反比例函数解析式为y=﹣ ![]() ,
,
∵OB=AB=1,
∴△OAB为等腰直角三角形,
∴∠AOB=45°,
∵PQ⊥OA,
∴∠OPQ=45°,
∵点B和点B′关于直线l对称,
∴PB=PB′,BB′⊥PQ,
∴∠B′PQ=∠OPQ=45°,∠B′PB=90°,
∴B′P⊥y轴,
∴点B′的坐标为(﹣ ![]() ,t),
,t),
∵PB=PB′,
∴t﹣1=|﹣ ![]() |=
|= ![]() ,
,
整理得t2﹣t﹣1=0,解得t1= ![]() ,t2=
,t2= ![]() (不符合题意,舍去),
(不符合题意,舍去),
∴t的值为 ![]() .
.
故选:A.
根据反比例函数图象上点的坐标特征由A点坐标为(﹣1,1)得到k=﹣1,即反比例函数解析式为y=﹣ ![]() ,且OB=AB=1,则可判断△OAB为等腰直角三角形,所以∠AOB=45°,再利用PQ⊥OA可得到∠OPQ=45°,然后轴对称的性质得PB=PB′,BB′⊥PQ,所以∠BPQ=∠B′PQ=45°,于是得到B′P⊥y轴,则点B′的坐标可表示为(﹣
,且OB=AB=1,则可判断△OAB为等腰直角三角形,所以∠AOB=45°,再利用PQ⊥OA可得到∠OPQ=45°,然后轴对称的性质得PB=PB′,BB′⊥PQ,所以∠BPQ=∠B′PQ=45°,于是得到B′P⊥y轴,则点B′的坐标可表示为(﹣ ![]() ,t),于是利用PB=PB′得t﹣1=|﹣
,t),于是利用PB=PB′得t﹣1=|﹣ ![]() |=
|= ![]() ,然后解方程可得到满足条件的t的值.
,然后解方程可得到满足条件的t的值.
-
科目: 来源: 题型:
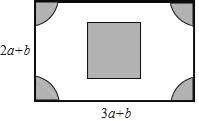
查看答案和解析>>【题目】如图,有一块长(3a+b)米,宽(2a+b)米的长方形广场,园林部门要对阴影区域进行绿化,空白区域进行广场硬化,其中,四个角部分是半径为(a﹣b)米的四个大小相同的扇形,中间部分是边长为(a+b)米的正方形.
(1)用含a、b的式子表示需要硬化部分的面积;
(2)若a=30,b=10,求出硬化部分的面积(结果保留π的形式).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线a、b、c表示三条公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有_______处.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AD平分∠BAC,DG⊥BC且平分BC,DE⊥AB于E,DF⊥AC于F.求证:BE=CF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】今年我市某公司分两次采购了一批大蒜,第一次花费40万元,第二次花费60万元,已知第一次采购时每吨大蒜的价格比去年的平均价格上涨了500元,第二次采购时每吨大蒜的价格比去年的平均价格下降了500元,第二次采购的数量是第一次采购数量的两倍.
(1)试问去年每吨大蒜的平均价格是多少元?
(2)该公司可将大蒜加工成蒜粉或蒜片,若单独加工成蒜粉,每天可加工8吨大蒜,每吨大蒜获利1000元;若单独加工成蒜片,每天可加工12吨大蒜,每吨大蒜获利600元.为出口需要,所有采购的大蒜必须在30天内加工完毕,且加工蒜粉的大蒜数量不少于加工蒜片的大蒜数量的一半.为获得最大利润,应将多少吨大蒜加工成蒜粉?最大利润为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题。
(1)计算:|﹣2|+2cos60°﹣(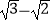 )0;
)0;
(2)解不等式: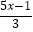 ﹣x>1,并将解集在数轴上表示出来.
﹣x>1,并将解集在数轴上表示出来. -
科目: 来源: 题型:
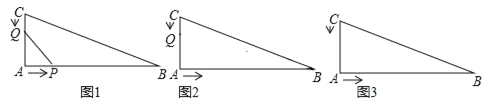
查看答案和解析>>【题目】在直角三角形ABC中,若AB=16cm,AC=12cm,BC=20cm.点P从点A开始以2厘米/秒的速度沿A→B→C的方向移动,点Q从点C开始以1厘米/秒的速度沿C→A→B的方向移动,如果点P、Q同时出发,用t(秒)表示移动时间,那么:
(1)如图1,请用含t的代数式表示,①当点Q在AC上时,CQ= ;②当点Q在AB上时,AQ= ;
③当点P在AB上时,BP= ;④当点P在BC上时,BP= .
(2)如图2,若点P在线段AB上运动,点Q在线段CA上运动,当QA=AP时,试求出t的值.
(3)如图3,当P点到达C点时,P、Q两点都停止运动,当AQ=BP时,试求出t的值.
相关试题

