【题目】已知,抛物线y=ax2+bx+3(a<0)与x轴交于A(3,0)、B两点,与y轴交于点C,抛物线的对称轴是直线x=1,D为抛物线的顶点,点E在y轴C点的上方,且CE= ![]() .
.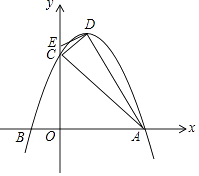
(1)求抛物线的解析式及顶点D的坐标;
(2)求证:直线DE是△ACD外接圆的切线;
(3)在直线AC上方的抛物线上找一点P,使S△ACP= ![]() S△ACD , 求点P的坐标;
S△ACD , 求点P的坐标;
(4)在坐标轴上找一点M,使以点B,C,M为顶点的三角形与△ACD相似,直接写出点M的坐标.
参考答案:
【答案】
(1)解:∵抛物线的对称轴是直线x=1,点A(3,0),
∴根据抛物线的对称性知点B的坐标为(﹣1,0),OA=3,
将A(3,0),B(﹣1,0)代入抛物线解析式中得: ![]() ,
,
解得: ![]() ,
,
∴抛物线解析式为y=﹣x2+2x+3;
当x=1时,y=4,
∴顶点D(1,4).
(2)解:当=0时,
∴点C的坐标为(0,3),
∴AC= ![]() =3
=3 ![]() ,CD=
,CD= ![]() =
= ![]() ,AD=
,AD= ![]() =2
=2 ![]() ,
,
∴AC2+CD2=AD2,
∴△ACD为直角三角形,∠ACD=90°.
∴AD为△ACD外接圆的直径,
∵点E在 轴C点的上方,且CE= ![]() .
.
∴E(0, ![]() )
)
∴AE= ![]() =
= ![]() DE=
DE= ![]() =
= ![]() ,
,
∴DE2+AD2=AE2,
∴△AED为直角三角形,∠ADE=90°.
∴AD⊥DE,
又∵AD为△ACD外接圆的直径,
∴DE是△ACD外接圆的切线;
(3)解:设直线AC的解析式为y=kx+b,
根据题意得: ![]() ,
,
解得: ![]() ,∴直线AC的解析式为y=﹣x+3,
,∴直线AC的解析式为y=﹣x+3,
∵A(3,0),D(1,4),
∴线段AD的中点N的坐标为(2,2),
过点N作NP∥AC,交抛物线于点P,
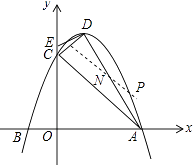
设直线NP的解析式为y=﹣x+c,
则﹣2+c=2,解得:c=4,
∴直线NP的解析式为y=﹣x+4,
由y=﹣x+4,y=﹣x2+2x+3联立得:﹣x2+2x+3=﹣x+4,
解得:x= ![]() 或x=
或x= ![]() ,
,
∴y= ![]() ,或y=
,或y= ![]()
∴P( ![]() ,
, ![]() )或(
)或( ![]() ,
, ![]() );
);
(4)解:分三种情况:①M恰好为原点,满足△CMB∽△ACD,M(0,0);
②M在x轴正半轴上,△MCB∽△ACD,此时M(9,0);
③M在y轴负半轴上,△CBM∽△ACD,此时M(0,﹣ ![]() );
);
综上所述,点M的坐标为(0,0)或(9,0)或(0,﹣ ![]() ).
).
【解析】(1)把A点坐标代入解析式及由对称轴x=1求出B点坐标代入即可;顶点可配方化为顶点式;(2)由两点间距离公式求出AC、CD、AD的长,运用勾股定理逆定理判定出△ACD为直角三角形,再判定出△AED为直角三角形,∠ADE=90°.即AD⊥DE,AD为△ACD外接圆的直径,所以DE是△ACD外接圆的切线;(3)若S△ACP= ![]() S△ACD则P在过AD中点的平行于AC的直线上,此直线解析式中k 与AC 解析式斜率k相等,联立此直线与抛物线解析式,求出P的坐标;(4)用文字连接的相似,对应点不确定,须分类讨论,分3类:M恰好为原点;M在x轴正半轴上;M在y轴负半轴上;按照对应边成比例,可求出M坐标.
S△ACD则P在过AD中点的平行于AC的直线上,此直线解析式中k 与AC 解析式斜率k相等,联立此直线与抛物线解析式,求出P的坐标;(4)用文字连接的相似,对应点不确定,须分类讨论,分3类:M恰好为原点;M在x轴正半轴上;M在y轴负半轴上;按照对应边成比例,可求出M坐标.
【考点精析】本题主要考查了相似三角形的判定与性质的相关知识点,需要掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线l1:y=2x+1、直线l2:y=﹣x+7,直线l1、l2分别交x轴于B、C两点,l1、l2相交于点A.
(1)求A、B、C三点坐标;
(2)求△ABC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】用棋子按照一定规律摆放图形
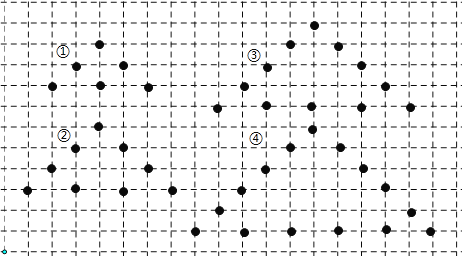
按照这种方式继续摆放下去,若摆放一个图形用去21枚棋子,则是摆放的第______个图形;摆放前n(n为正整数)个图形共需用______枚棋子.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,所给图形中是中心对称图形但不是轴对称图形的是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国是世界上严重缺水的国家之一.为了增强居民的节水意识,某市自来水公司对居民用水采用以户为单位分段计费办法收费.即一个月用水10 t以内(包括10 t)的用户,每吨收水费a元;一个月用水超过10 t的用户,10 t水仍按每吨a元收费,超过10 t的部分,按每吨b(b>a)元收费.设一户居民月用水x t,应交水费y元,y与x之间的函数关系如图所示.
(1)求a的值;某户居民上月用水8 t,应交水费多少元?
(2)求b的值,并写出当x>10时,y与x之间的函数表达式.

-
科目: 来源: 题型:
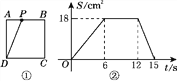
查看答案和解析>>【题目】如图①所示,正方形ABCD的边长为6 cm,动点P从点A出发,在正方形的边上沿A→B→C→D运动,设运动的时间为t(s),三角形APD的面积为S(cm2),S与t的函数图象如图②所示,请回答下列问题:
(1)点P在AB上运动的时间为________s,在CD上运动的速度为________cm/s,三角形APD的面积S的最大值为________cm2;
(2)求出点P在CD上运动时S与t之间的函数表达式;
(3)当t为何值时,三角形APD的面积为10 cm2?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某工厂有甲、乙两个大小相同的蓄水池,且中间有管道连通,现要向甲池中注水,若单位时间内的注水量不变,那么从注水开始,乙水池水面上升的高度h与注水时间t之间的函数关系图象可能是( )
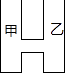
A.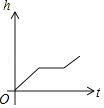
B.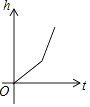
C.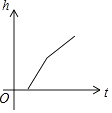
D.
相关试题

