搜索
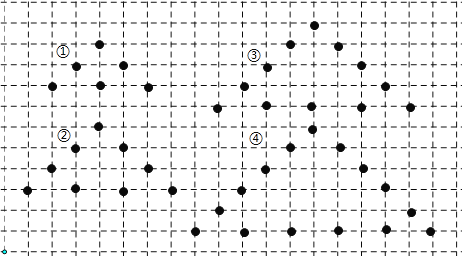
【题目】如图，所给图形中是中心对称图形但不是轴对称图形的是（ ）
A.
B.
C.
D.
参考答案：
【答案】C
【解析】解：A、不是轴对称图形，也不是中心对称图形．故A选项错误；
B、是轴对称图形，也是中心对称图形．故B选项错误；
C、不是轴对称图形，是中心对称图形．故C选项正确；
D、是轴对称图形，不是中心对称图形．故D选项错误．
所以答案是：C．
【考点精析】根据题目的已知条件，利用轴对称图形和中心对称及中心对称图形的相关知识可以得到问题的答案，需要掌握两个完全一样的图形关于某条直线对折，如果两边能够完全重合，我们就说这两个图形成轴对称，这条直线就对称轴；如果把一个图形绕着某一点旋转180度后能与另一个图形重合，那么我们就说，这两个图形成中心对称；如果把一个图形绕着某一点旋转180度后能与自身重合，那么我们就说，这个图形成中心对称图形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】甲、乙两组工人同时加工某种零件，乙组工作中有一次停产更换设备，更换设备
后，乙组的工作效率是原来的2倍．两组各自加工零件的数量
(件)与时间
(时)的函数图象如图所示．
（1）求甲组加工零件的数量y与时间
之间的函数关系式．（2分）（2）求乙组加工零件总量
的值．（3分）（3）甲、乙两组加工出的零件合在一起装箱，每够300件装一箱，零件装箱的时间忽略不计，求经过多长时间恰好装满第1箱？再经过多长时间恰好装满第2箱？（5分）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知直线l1：y＝2x+1、直线l2：y＝﹣x+7，直线l1、l2分别交x轴于B、C两点，l1、l2相交于点A．
（1）求A、B、C三点坐标；
（2）求△ABC的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】用棋子按照一定规律摆放图形
按照这种方式继续摆放下去，若摆放一个图形用去21枚棋子，则是摆放的第______个图形；摆放前n（n为正整数）个图形共需用______枚棋子．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知，抛物线y=ax2+bx+3（a＜0）与x轴交于A（3，0）、B两点，与y轴交于点C，抛物线的对称轴是直线x=1，D为抛物线的顶点，点E在y轴C点的上方，且CE=
．
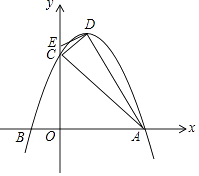
（1）求抛物线的解析式及顶点D的坐标；
（2）求证：直线DE是△ACD外接圆的切线；
（3）在直线AC上方的抛物线上找一点P，使S△ACP= S△ACD ， 求点P的坐标；
（4）在坐标轴上找一点M，使以点B，C，M为顶点的三角形与△ACD相似，直接写出点M的坐标． -
科目： 来源： 题型：
查看答案和解析>>【题目】我国是世界上严重缺水的国家之一．为了增强居民的节水意识，某市自来水公司对居民用水采用以户为单位分段计费办法收费．即一个月用水10 t以内(包括10 t)的用户，每吨收水费a元；一个月用水超过10 t的用户，10 t水仍按每吨a元收费，超过10 t的部分，按每吨b(b＞a)元收费．设一户居民月用水x t，应交水费y元，y与x之间的函数关系如图所示．
(1)求a的值；某户居民上月用水8 t，应交水费多少元？
(2)求b的值，并写出当x＞10时，y与x之间的函数表达式．
-
科目： 来源： 题型：
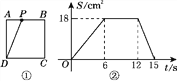
查看答案和解析>>【题目】如图①所示，正方形ABCD的边长为6 cm，动点P从点A出发，在正方形的边上沿A→B→C→D运动，设运动的时间为t(s)，三角形APD的面积为S(cm2)，S与t的函数图象如图②所示，请回答下列问题：
(1)点P在AB上运动的时间为________s，在CD上运动的速度为________cm/s，三角形APD的面积S的最大值为________cm2；
(2)求出点P在CD上运动时S与t之间的函数表达式；
(3)当t为何值时，三角形APD的面积为10 cm2?
相关试题
