【题目】发现:
任意三个连续偶数的平方和是![]() 的倍数.
的倍数.
验证:
(1)![]() 的结果是
的结果是![]() 的几倍?
的几倍?
(2)设三个连续偶数的中间一个为![]() ,写出它们的平方和,并说明是
,写出它们的平方和,并说明是![]() 的倍数.
的倍数.
延伸:
(3)任意三个连续奇数的平方和,设中间一个为![]() ,被
,被![]() 整除余数是几呢?请写出理由.
整除余数是几呢?请写出理由.
参考答案:
【答案】(1)14倍;(2)见解析;(3)被![]() 整除后,余数为
整除后,余数为![]() .
.
【解析】
(1)直接计算出算式的结果除以4即可得答案;(2)由三个连续偶数的中间一个为![]() ,可得三个偶数为2n-2、2n、2n+2,计算出三个数的和即可得答案;(3)由三个连续奇数的中间一个为
,可得三个偶数为2n-2、2n、2n+2,计算出三个数的和即可得答案;(3)由三个连续奇数的中间一个为![]() +1,可得三个偶数为2n-1、2n+1、2n+3,计算出三个数的和即可得答案.
+1,可得三个偶数为2n-1、2n+1、2n+3,计算出三个数的和即可得答案.
(1)(22+42+62)÷4=56÷4=14(倍).
∴![]() 的结果是
的结果是![]() 的14倍.
的14倍.
(2)∵三个连续偶数为2n-2、2n、2n+2,
∴![]() ,
,
∴是![]() 的倍数.
的倍数.
(3)∵三个连续奇数为2n-1、2n+1、2n+3,
∴![]() =12(n+1)+11
=12(n+1)+11
∴被![]() 整除后,余数为
整除后,余数为![]() ;
;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
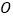 、
、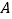 在数轴上表示的数分别是
在数轴上表示的数分别是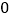 ,
,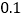 ,将线段
,将线段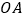 分成
分成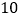 等分,离
等分,离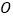 点最近的分点为
点最近的分点为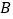 ;再将线段
;再将线段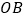 分成
分成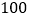 等份,其分点由左向右依次为
等份,其分点由左向右依次为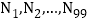 ;继续将线段
;继续将线段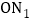 分成
分成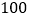 等份,其分点由左向右依次为
等份,其分点由左向右依次为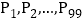 ;
;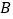 对应的数用科学记数法表示为:________;
对应的数用科学记数法表示为:________;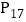 对应的数用科学记数法表示为:______.
对应的数用科学记数法表示为:______.
-
科目: 来源: 题型:
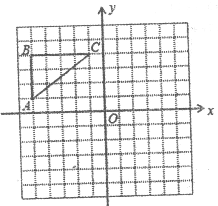
查看答案和解析>>【题目】如图,在正方形网络中,△ABC各顶点都在格点上,点A,C的坐标分别为(-5,1)、(-1,4),结合所给的平面直角坐标系解答下列问题:
画出△ABC关于
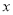 轴对称的△A1B1C1;
轴对称的△A1B1C1;画出△ABC关于原点O对称的△A2B2C2;
点C1的坐标是 ;点C2的坐标是 ;
试判断:△A1B1C1与△A2B2C2是否关于y轴对称?(只需写出判断结果)
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面的推理填空
如图,已知
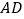 是
是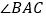 的角平分线,
的角平分线,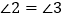 ,试证明:
,试证明: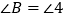 .
.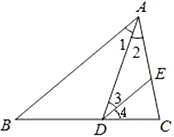
证明:
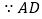 是
是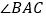 的角平分线(已知)
的角平分线(已知) ___________( )
___________( )又
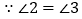 (已知)
(已知) ___________( )
___________( ) ___________( )
___________( ) ___________( )
___________( ) -
科目: 来源: 题型:
查看答案和解析>>【题目】世界上大部分国家都使用摄氏温度(
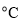 ),但美国、英国等国家的天气预报仍然使用华氏温度(
),但美国、英国等国家的天气预报仍然使用华氏温度(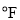 ).两种计量之间有如下对应:
).两种计量之间有如下对应:摄氏温度(
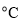 )
)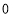
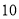
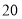
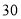

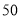
华氏温度(
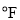 )
)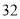

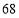

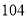
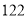
(1)上表反映了哪两变量之间的关系?哪个是自变量?哪个是因变量?
(2)由上表可得:摄氏温度(
 )每提高
)每提高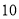 度,华氏温度(
度,华氏温度(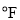 )提高_____度.
)提高_____度.(3)摄氏温度
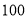 度时华氏温度为______度.
度时华氏温度为______度.(4)华氏温度
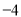 度时摄氏温度为_______度.
度时摄氏温度为_______度.(5)华氏温度的值与对应的摄氏温度的值有相等的可能吗?如果有,求出这个值.如果没有,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】省射击队为从甲、乙两名运动员中选拔一人参加全国比赛,对
他们进行了六次测试,测试成绩如下表(单位:环):
第一次
第二次
第三次
第四次
第五次
第六次
甲
10
8
9
8
10
9
乙
10
7
10
10
9
8
(1)根据表格中的数据,计算出甲的平均成绩是 环,乙的平均成绩是 环;
(2)分别计算甲、乙六次测试成绩的方差;
(3)根据(1)、(2)计算的结果,你认为推荐谁参加全国比赛更合适,请说明理由.
(计算方差的公式:s2=
 [
[ ])
]) -
科目: 来源: 题型:
查看答案和解析>>【题目】每年九月是开学季,大多数学生会购买若干笔记本满足日常学习需要,校外某文具店老板开学前某日去批发市场进货,购进甲乙丙三种不同款式的笔记本,已知甲款笔记本的进价为2元/本,乙款笔记本的进价为4元/本,丙款笔记本的进价为6元/本,经过调研发现,甲款笔记本、乙款笔记本和丙款笔记本的零售价分别定为4元/本、6元/本和10元/本时,每天可分别售出甲款笔记本30本、乙款笔记本50本和丙款笔记本20本,如果将乙款笔记本的零售价提高
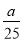 元(
元(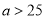 ),甲款笔记本和丙款笔记本的零售价均保持不变,那么乙款笔记本每天的销售量将下降
),甲款笔记本和丙款笔记本的零售价均保持不变,那么乙款笔记本每天的销售量将下降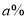 ,丙款笔记本每天的销售量将上升
,丙款笔记本每天的销售量将上升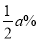 ,甲款笔记本每天的销量仍保持不变.
,甲款笔记本每天的销量仍保持不变.(1)若
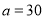 ,调价后每天销售三款笔记本共可获利多少元?
,调价后每天销售三款笔记本共可获利多少元?(2)若调价后每天销售三款笔记本共可获利260元,求
 的值.
的值.
相关试题

