搜索
【题目】已知三角形的三条边长均为整数，其中有 一条边长是4，其余两边均不超过4，这样的三角形的个数有几个（ ）．
A.3B.4C.5D.6
参考答案：
【答案】D
【解析】
解：根据三角形边长的性质，可得出三角形有2、3、4；3、3、4；2、4、4；1、4、4；3、4、4；4、4、4共六种可能，
故选D．
-
科目： 来源： 题型：
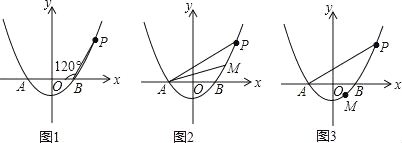
查看答案和解析>>【题目】(2016湖南省邵阳市第26题)已知抛物线y=ax2﹣4a（a＞0）与x轴相交于A，B两点（点A在点B的左侧），点P是抛物线上一点，且PB=AB，∠PBA=120°，如图所示．
（1）求抛物线的解析式．
（2）设点M（m，n）为抛物线上的一个动点，且在曲线PA上移动．
①当点M在曲线PB之间（含端点）移动时，是否存在点M使△APM的面积为
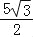？若存在，求点M的坐标；若不存在，请说明理由．②当点M在曲线BA之间（含端点）移动时，求|m|+|n|的最大值及取得最大值时点M的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】当x＝m或x＝n（m≠n）时，代数式x2﹣2x+4的值相等，则当x＝m+n时，代数式x2﹣2x+4的值为_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】方程x+5=2x﹣3的解是________．
-
科目： 来源： 题型：
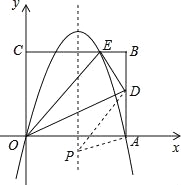
查看答案和解析>>【题目】(2016广西省贺州市第26题)如图，矩形的边OA在x轴上，边OC在y轴上，点B的坐标为（10，8），沿直线OD折叠矩形，使点A正好落在BC上的E处，E点坐标为（6，8），抛物线y=ax2+bx+c经过O、A、E三点．
（1）求此抛物线的解析式；
（2）求AD的长；
（3）点P是抛物线对称轴上的一动点，当△PAD的周长最小时，求点P的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点B和点C分别为∠MAN两边上的点，AB=AC.
（1）按下列语句画出图形：(要求不写作法，保留作图痕迹)
① AD⊥BC，垂足为D；
② ∠BCN的平分线CE与AD的延长线交于点E；
③ 连结BE.
（2）在完成（1）后不添加线段和字母的情况下，请你写出除△ABD≌△ACD外的两对全等三角形： ≌ ， ≌ ；并选择其中的一对全等三角形予以证明.
-
科目： 来源： 题型：
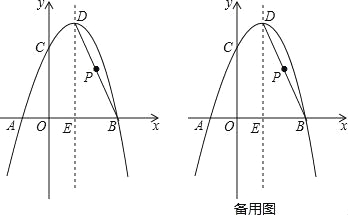
查看答案和解析>>【题目】(2016广东省茂名市第25题)如图，抛物线y=﹣x2+bx+c经过A（﹣1，0），B（3，0）两点，且与y轴交于点C，点D是抛物线的顶点，抛物线的对称轴DE交x轴于点E，连接BD．
（1）求经过A，B，C三点的抛物线的函数表达式；
（2）点P是线段BD上一点，当PE=PC时，求点P的坐标；
（3）在（2）的条件下，过点P作PF⊥x轴于点F，G为抛物线上一动点，M为x轴上一动点，N为直线PF上一动点，当以F、M、G为顶点的四边形是正方形时，请求出点M的坐标．
相关试题
