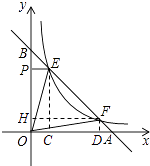
【题目】如图,点E,F在函数y= ![]() (x>0)的图象上,直线EF分别与x轴、y轴交于点A,B,且BE:BF=1:m.过点E作EP⊥y轴于P,已知△OEP的面积为1,则k值是 , △OEF的面积是(用含m的式子表示)
(x>0)的图象上,直线EF分别与x轴、y轴交于点A,B,且BE:BF=1:m.过点E作EP⊥y轴于P,已知△OEP的面积为1,则k值是 , △OEF的面积是(用含m的式子表示)
参考答案:
【答案】2;![]()
【解析】解:作EC⊥x轴于C,FD⊥x轴于D,FH⊥y轴于H,如图,
∵△OEP的面积为1,
∴ ![]() |k|=1,
|k|=1,
而k>0,
∴k=2,
∴反比例函数解析式为y= ![]() ,
,
∵EP⊥y轴,FH⊥y轴,
∴EP∥FH,
∴△BPE∽△BHF,
∴ ![]() =
= ![]() ,即HF=mPE,
,即HF=mPE,
设E点坐标为(t, ![]() ),则F点的坐标为(tm,
),则F点的坐标为(tm, ![]() ),
),
∵S△OEF+S△OFD=S△OEC+S梯形ECDF ,
而S△OFD=S△OEC=1,
∴S△OEF=S梯形ECDF= ![]() (
( ![]() +
+ ![]() )(tm﹣t)
)(tm﹣t)
=( ![]() +1)(m﹣1)
+1)(m﹣1)
= ![]() .
.
所以答案是:2, ![]() .
.
【考点精析】掌握反比例函数的性质是解答本题的根本,需要知道性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2﹣(m+2)x+2m=0
(1)求证:不论m为何值,该方程总有两个实数根;
(2)若此方程的一个根是1,请求出方程的另一个根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:4﹣x2= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某村耕地总面积为50公顷,且该村人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数图象如图所示,则下列说法正确的是( )

A.该村人均耕地面积随总人口的增多而增多
B.当该村总人口为50人时,人均耕地面积为1公顷
C.若该村人均耕地面积为2公顷,则总人口有100人
D.该村人均耕地面积y与总人口x成正比例 -
科目: 来源: 题型:
查看答案和解析>>【题目】若正比例函数y=kx(k为常数,且k≠0)的函数值y随着x的增大而减小,则k的值可以是 . (写出一个即可)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,D是BC边上一点,以DB为直径的⊙O经过AB的中点E,交AD的延长线于点F,连结EF.
(1)求证:∠1=∠F;
(2)若sinB=
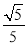 ,EF=
,EF=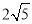 ,求CD的长.
,求CD的长.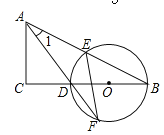
-
科目: 来源: 题型:
查看答案和解析>>【题目】
【发现】
如图∠ACB=∠ADB=90°,那么点D在经过A,B,C三点的圆上(如图①)
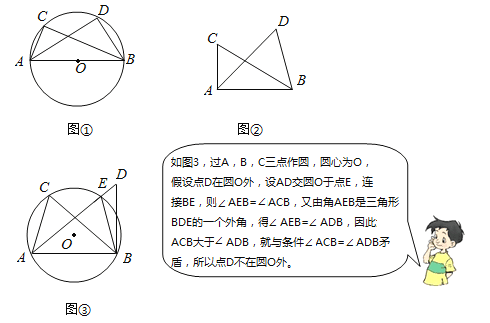
【思考】
如图②,如果∠ACB=∠ADB=a(a≠90°)(点C,D在AB的同侧),那么点D还在经过A,B,C三点的圆上吗?
请证明点D也不在⊙O内.
【应用】
利用【发现】和【思考】中的结论解决问题:若四边形ABCD中,AD∥BC,∠CAD=90°,点E在边AB上,CE⊥DE.
(1)作∠ADF=∠AED,交CA的延长线于点F(如图④),求证:DF为Rt△ACD的外接圆的切线;
(2)如图⑤,点G在BC的延长线上,∠BGE=∠BAC,已知sin∠AED=
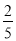 ,AD=1,求DG的长.
,AD=1,求DG的长.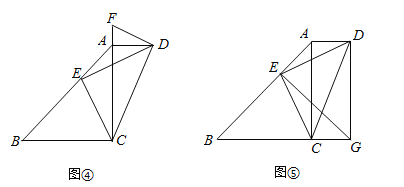
相关试题

