【题目】将等腰直角△ABC斜放在平面直角坐标系中,使直角顶点C与点(1,0)重合,点A的坐标为(﹣2,1).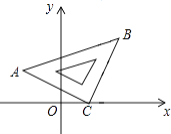
(1)求△ABC的面积S;
(2)求直线AB与y轴的交点坐标.
参考答案:
【答案】
(1)解:过点A作AD⊥x轴,垂足为D.
∵C(1,0),A(﹣2,1),
∴AD=1,DC=1﹣(﹣2)=3,
∴AC2=AD2+DC2=10,
∴S△ABC= ![]() AC2=5
AC2=5
(2)解:过点B作BE⊥x轴,垂足为E, 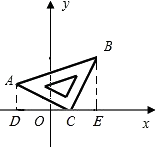
∴∠ADC=∠CEB=90°,
∴∠CAD+∠ACD=90°,
∵∠ACB=90°,
∴∠BCE+∠ACD=90°,
∴∠CAD=∠BCE.
在△ADC和△CEB中,
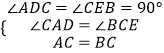 ,
,
∴△ADC≌△CEB,
∴CD=BE=3,CE=AD=1,
∴OE=2,
∴点B的坐标为(2,3).
设直线AB的解析式为y=kx+b,则
![]() ,
,
解得 ![]() ,
,
∴y= ![]() x+2.
x+2.
当x=0时,y=2,
∴直线AB交y轴于点(0,2).
【解析】(1)过点A作AD⊥x轴,垂足为D,由C,D两点的坐标得出AD,DC的长然后用勾股定理得出AC的长,利用直角三角形的面积计算方法得出答案;
(2)过点B作BE⊥x轴,垂足为E,根据直角三角形两锐角互余,及同角的余角相等得出∠CAD=∠BCE,然后由AAS得出△ADC≌△CEB,根据全等三角形的性质得出CD=BE=3,CE=AD=1,故OE=2,从而得出B点的坐标,用待定系数法求出直线AB的解析式,进而求出直线AB与y轴交点的坐标。
【考点精析】关于本题考查的确定一次函数的表达式和勾股定理的概念,需要了解确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解我市中学生跳绳活动开展的情况,随机抽查了全市八年级部分同学1分钟跳绳的次数,将抽查结果进行统计,并绘制成如下的两个不完整的统计图:
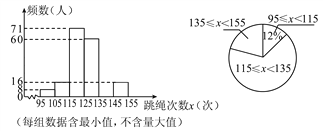
请根据图中提供的信息,解答下列问题:
(1)本次共抽查了多少名学生?
(2)请补全频数分布直方图;
(3)若本次抽查中,跳绳次数在125次以上(含125次)为优秀,请你估计全市8000名八年级学生中有多少名学生的成绩为优秀;
(4)请你根据以上信息,对我市开展的学生跳绳活动情况谈谈自己的看法或建议.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2017年度中央机关及其直属机构公务员招考网上报名已经结束,据初步统计,网上报名人数约有211.5万人,数据211.5万用科学记数法可表示为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的袋中装有20个球,其中7个黄球,8个黑球,5个红球,这些球只有颜色不同,其它都相同.
(1)求从袋中摸出一个球是黄球的概率;
(2)现从袋中取出若干个黑球,搅匀后,使从袋中摸出一个球是黑球的概率是 ,求从袋中取出黑球的个数.
,求从袋中取出黑球的个数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,反比例函数y=
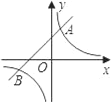
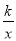 的图象与一次函数y=mx+b的图象交于A(1,3),B(n,﹣1)两点.
的图象与一次函数y=mx+b的图象交于A(1,3),B(n,﹣1)两点.(1)求反比例函数与一次函数的解析式;
(2)根据图象回答:当x取何值时,反比例函数的值大于一次函数的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某服装店将原来每件m元的服装加价50%后销售,由于转季,服装店将该服装降价40%,则经过降价后每件服装的价格为元(结果用含m的代数式表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果x1与x2的平均数是4,那么x1+1与x2+5的平均数是 ▲ .
相关试题

