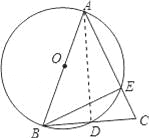
【题目】如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D, AC交⊙O于点E,∠BAC=45°。
(1)求∠EBC的度数;
(2)求证:BD=CD。

参考答案:
【答案】(1)∠EBC=22.5°.(2)证明见解析
【解析】试题分析:(1)∠EBC的度数等于∠ABC﹣∠ABE,因而求∠EBC的度数就可以转化为求∠ABC和∠ABE,根据等腰三角形的性质等边对等角,就可以求出.
(2)在等腰三角形ABC中,根据三线合一定理即可证得.
试题解析:(1)∵AB是⊙O的直径,
∴∠AEB=90°.
又∵∠BAC=45°,
∴∠ABE=45°.
又∵AB=AC,
∴∠ABC=∠C=67.5°.
∴∠EBC=22.5°.
(2)连接AD,
∵AB是⊙O的直径,
∴∠ADB=90°.
∴AD⊥BC.
又∵AB=AC,
∴BD=CD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数
 的图象如图所示,则①
的图象如图所示,则①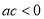 ;②
;② ;③
;③ ;④
;④ ;⑤4a+2b+c>0;⑥a+b+c>0上述六个结论中正确的有( )
;⑤4a+2b+c>0;⑥a+b+c>0上述六个结论中正确的有( )
A. 两个 B. 三个 C. 四个 D. 五个
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算3x2+2x2的结果( )
A.5B.5x2C.5x4D.6x2
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分10分)如图,△ABC是⊙O的内接三角形,AD是⊙O的直径,∠ABC=60°,∠ACB=50°,请解答下列问题:

(1)求∠CAD的度数;
(2)设AD、BC相交于E,AB、CD的延长线相交于F,求∠AEC、∠AFC的度数;
(3)若AD=6,求图中阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将二次函数y=x2的图象向上平移m(m>0)个单位再向右平移2个单位,则平移以后的二次函数的解析式为( )
A.y=(x+2)2﹣mB.y=(x+2)2+mC.y=(x+m)2+2D.y=(x﹣2)2+m
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分10分)九年级数学兴趣小组经过市场调查,得到某种运动服每月的销量与售价的相关信息如下表:
售价(元/件)
100
110
120
130
…
月销量(件)
200
180
160
140
…
已知该运动服的进价为每件60元,设售价为x元.
(1)请用含x的式子表示:①销售该运动服每件的利润是 (__________)元;②月销量是 (__________)件;(直接写出结果)
(2)设销售该运动服的月利润为y元,那么售价为多少时,当月的利润最大,最大利润是多少?
相关试题

