【题目】如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E,F分别在BC和CD上.下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF;④S正方形ABCD=2+ ![]() .其中正确的个数为( )
.其中正确的个数为( ) 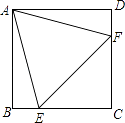
A.1
B.2
C.3
D.4
参考答案:
【答案】C
【解析】解:∵四边形ABCD是正方形,
∴AB=AD,
∵△AEF是等边三角形,
∴AE=AF,
在Rt△ABE和Rt△ADF中,![]() ,
,
∴Rt△ABE≌Rt△ADF(HL),
∴BE=DF,
∵BC=DC,
∴BC﹣BE=CD﹣DF,
∴CE=CF,
∴①说法正确;
∵CE=CF,
∴△ECF是等腰直角三角形,
∴∠CEF=45°,
∵∠AEF=60°,
∴∠AEB=75°,
∴②说法正确;
如图,连接AC,交EF于G点,
∴AC⊥EF,且AC平分EF,
∵∠CAF≠∠DAF,
∴DF≠FG,
∴BE+DF≠EF,
∴③说法错误;
∵EF=2,
∴CE=CF= ![]() ,
,
设正方形的边长为a,
在Rt△ADF中,
a2+(a﹣ ![]() )2=4,
)2=4,
解得a= ![]() ,
,
则a2=2+ ![]() ,
,
∴S正方形ABCD=2+ ![]() ,
,
④说法正确,
∴正确的有①②④.
故选C.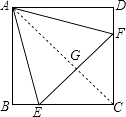
根据三角形的全等的知识可以判断①的正误;根据角角之间的数量关系,以及三角形内角和为180°判断②的正误;根据线段垂直平分线的知识可以判断③的正误,利用解三角形求正方形的面积等知识可以判断④的正误.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1) ﹣
﹣ 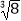 ﹣(π﹣1)0
﹣(π﹣1)0
(2)(﹣2a2b)2(6ab)÷(﹣3b2)
(3)(2x﹣1)(3x+2)﹣6x(x﹣2)
(4)(3x﹣y)2﹣(3x+2y)(3x﹣2y) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,MN是⊙O的直径,MN=10,点A在⊙O上,∠AMN=30°,B为弧AN的中点,P是直径MN上一动点,则PA+PB的最小值为__________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在锐角△ABC中,AB=6,∠BAC=45°,∠BAC的平分线交BC于点D,M,N分别是AD和AB上的动点,则BM+MN的最小值是( )

A.
B.6
C.
D.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场购进枇杷20吨,桃子12吨.现计划租用甲、乙两种货车共8辆将这批水果运回,已知一辆甲种货车可装枇杷4吨和桃子1吨,一辆乙种货车可装枇杷和桃子各2吨.
(1)如何安排甲、乙两种货车可一次性地运到?有几种方案?
(2)若甲种货车每辆要付运输费300元,乙种货车每辆要付运输费240元,则果商场应选择哪种方案,使运输费最少?最少运费是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列关于四边形的说法,正确的是( )
A. 四个角相等的菱形是正方形 B. 对角线互相垂直的四边形是菱形
C. 有两边相等的平行四边形是菱形 D. 两条对角线相等的四边形是菱形
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=﹣x2+2x﹣4,当﹣1<x<2时,y的取值范围是( )
A.﹣7<y<﹣4B.﹣7<y≤﹣3C.﹣7≤y<﹣3D.﹣4<y≤﹣3
相关试题

