【题目】某商场购进枇杷20吨,桃子12吨.现计划租用甲、乙两种货车共8辆将这批水果运回,已知一辆甲种货车可装枇杷4吨和桃子1吨,一辆乙种货车可装枇杷和桃子各2吨.
(1)如何安排甲、乙两种货车可一次性地运到?有几种方案?
(2)若甲种货车每辆要付运输费300元,乙种货车每辆要付运输费240元,则果商场应选择哪种方案,使运输费最少?最少运费是多少?
参考答案:
【答案】解:(1)设安排甲种货车x辆,则安排乙种货车(8-x)辆,依题意,
得:4x + 2(8-x)≥20,且x + 2(8-x)≥12,
解此不等式组,得 x≥2,且 x≤4,即 2≤x≤4
∵ x是正整数,∴ x可取的值为2,3,4.
因此安排甲、乙两种货车有三种方案:
甲种货车 | 乙种货车 | |
方案一 | 2辆 | 6辆 |
方案二 | 3辆 | 5辆 |
方案三 | 4辆 | 4辆 |
(2)方案一所需运费 300×2 + 240×6 = 2040元;
方案二所需运费 300×3 + 240×5 = 2100元;
方案三所需运费 300×4 + 240×4 = 2160元.
所以商场应选择方案一运费最少,最少运费是2040元.
【解析】(1)本题可设甲、乙货车的辆数分别为x和8-x,然后根据题意列出不等式:4x+2(8-x)≥20和x+2(8-x)≥12,化简后得出x的取值范围,看其中有几个整数即可得知有几种方案.
(2)本题可根据第一题列出的几种方案分别计算甲、乙所需的运费,比较哪个少即可得出答案.
解:(1)设安排甲种货车x辆,则安排乙种货车(8-x)辆,依题意得
![]()
解此不等式组得x≥2,且x≤4,即2≤x≤4,
∵x是正整数,
∴x可取的值为2,3,4,
因此安排甲、乙两种货车有三种方案:

(2)方案一所需运费为300×2+240×6=2040元;
方案二所需运费为300×3+240×5=2100元;
方案三所需运费为300×4+240×4=2160元,
所以张三应选择方案一运费最少,最少运费是2040元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某县九年级有15000名学生参加安全应急预案知识竞赛活动,为了了解本次知识竞赛的成绩分布情况,从中抽取了400名学生的得分(得分取正整数,满分100分)进行统计:
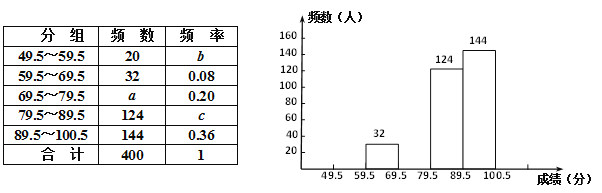
请结合图表完成下列问题:
(1)表中的
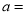 ,b= , c= ;
,b= , c= ;(2)请把频数分布直方图补充完整;
(3)若将得分转化为等级,规定得分低于59.5分评为“D”,59.5~69.5分评为“C”,69.5~89.5分评为“B”,89.5~100.5分评为“A”,这次15000名学生中约有多少人被评为“B”?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店需要购进一批电视机和洗衣机,根据市场调查,决定电视机进货量不少于洗衣机进货量的一半.电视机与洗衣机的进价和售价如下表:
类 别
电视机
洗衣机
进价(元/台)
1 800
1 500
售价(元/台)
2 000
1 600
计划购进电视机和洗衣机共 100 台,商店最多可筹集资金161 800 元.
(1)请你帮助商店算一算有多少种进货方案(不考虑除进价之外的其他费用);
(2)哪种进货方案待商店销售购进的电视机与洗衣机完毕后获得的利润最多?并求出最大的利润(利润=售价-进价).
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次数学测试中,小明所在小组的5个同学的成绩(单位:分)分别是:90、91、88、90、97,则这组数据的中位数是( )
A. 88 B. 90 C. 90.5 D. 91
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程x2+9x+9=0的两根为x1,x2,则x1+x2﹣x1x2=( )
A.﹣18B.18C.9D.0
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,点O为坐标原点,抛物线y=mx2﹣6mx+5m与x轴交于A、B两点,与y轴交于点C,
 =
=  .
.
(1)求m的值;
(2)如图2,连接BC,点P为点B右侧的抛物线上一点,连接PA并延长交y轴于点D,过点P作PF⊥x轴于F,交线段CB的延长线于点E,连接DE,求证:DE∥AB;
(3)在(2)的条件下,点G在线段PE上,连接DG,若EG=2PG,∠DPE=2∠GDE时,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某水库的水位下降1米,记作﹣1米,那么+1.2米表示 .
相关试题

