【题目】已知一条抛物线经过A(0,3),B(4,6)两点,对称轴是x=.

(1)求这条抛物线的关系式.

(2)证明:这条抛物线与x轴的两个交点中,必存在点C,使得对x轴上任意点D都有AC+BC≤AD+BD.

参考答案：

【答案】（1）y=.（2）证明见解析.

【解析】本题主要考查了抛物线与x轴的交点和待定系数法求二次函数解析式

（1）先设出函数的解析式：y=ax2+bx+c，根据抛物线经过A（0，3），B（4，6）两点，用待定系数法求出函数的解析式；

（2）令y=0，得到方程，根据方程根与系数的关系求出抛物线与x轴的两个交点，再根据三角形任意两边之和大于第三边，来证明．

(1)解:设所求抛物线的关系式为y=ax2+bx+c,

∵A(0,3),B(4,6),对称轴是直线x=.

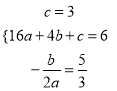∴, 解得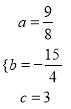

∴y=.

(2)证明:令y=0,得="0," ∴

∵A(0,3),取A点关于x轴的对称点E,∴E (0,-3).

设直线BE的关系式为y=kx-3,把B(4,6)代入上式,得6=4k-3,

∴k=,∴y=x-3 .

由x-3=0,得x=.

故C为,C点与抛物线在x轴上的一个交点重合,

在x轴上任取一点D,在△BED中,BE< BD+DE.

又∵BE=EC+BC,EC=AC,ED=AD,∴AC+BC<AD+BD.

若D与C重合,则AC+BC="AD+BD." ∴AC+BC≤AD+BD.

关闭