【题目】(本题满分10分)如图,在平行四边形ABCD中,点A、B、C的坐标分别是(1,0)、(3,1)、(3,3),双曲线y=![]() (k≠0,x>0)过点D.
(k≠0,x>0)过点D.
(1)求此双曲线的解析式;
(2)作直线AC交y轴于点E,连结DE,求△ CDE的面积.

参考答案:
【答案】(1)![]() ;(2)3.
;(2)3.
【解析】试题分析:(1)根据在平行四边形ABCD中,点A、B、C的坐标分别是(1,0)、(3,1)、(3,3),可以求得点D的坐标,又因为双曲线![]() (k≠0,x>0)过点D,从而可以求得k的值,从而可以求得双曲线的解析式;
(k≠0,x>0)过点D,从而可以求得k的值,从而可以求得双曲线的解析式;
(2)由图可知三角形CDE的面积等于三角形EDA与三角形ADC的面积之和,从而可以解答本题.
试题解析:(1)∵在平行四边形ABCD中,点A、B、C的坐标分别是(1,0)、(3,1)、(3,3),∴点D的坐标是(1,2),∵双曲线![]() (k≠0,x>0)过点D,∴2=
(k≠0,x>0)过点D,∴2=![]() ,得k=2,即双曲线的解析式是:
,得k=2,即双曲线的解析式是: ![]() ;
;
(2)∵直线AC交y轴于点E,∴S△CDE=S△EDA+S△ADC=![]() =1+2=3,即△CDE的面积是3.
=1+2=3,即△CDE的面积是3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设A(﹣2,y1),B(1,y2),C(2,y3)是抛物线y=﹣(x+1)2+k上的三点,则y1 , y2 , y3的大小关系为( )
A.y1>y2>y3
B.y1>y3>y2
C.y2>y3>y1
D.y3>y1>y2 -
科目: 来源: 题型:
查看答案和解析>>【题目】八(2)班组织了一次经典朗读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲
7
8
9
7
10
10
9
10
10
10
乙
10
8
7
9
8
10
10
9
10
9
(1)甲队成绩的中位数是分,乙队成绩的众数是分;
(2)计算甲队的平均成绩和方差;
(3)已知乙队成绩的方差是1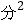 ,则成绩较为整齐的是哪一队.
,则成绩较为整齐的是哪一队. -
科目: 来源: 题型:
查看答案和解析>>【题目】探究题:
 =3,
=3, 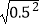 =0.5,
=0.5, 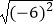 =6,
=6, 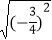 =
=  ,
,  =0.
=0.
根据以上算式,回答:
(1)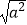 一定等于a吗?如果不是,那么
一定等于a吗?如果不是,那么 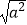 =;
=;
(2)利用你总结的规律,计算: ①若x<2,则 =;
=;
②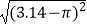 = .
= .
(3)若a,b,c为三角形的三边长,化简: +
+ 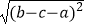 +
+ 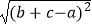 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】设“○”、“□”、“△”分别表示三种不同的物体,用天平比较它们质量的大小,两次情况如图所示,那么每个“○”、“□”、“△”这样的物体,按质量从小到大的顺序排列为( )
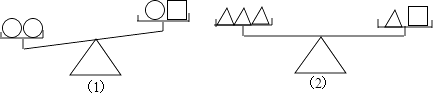
A.○□△
B.○△□
C.□○△
D.△□○ -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中是真命题的为( )
A. 弦是直径
B. 直径相等的两个圆是等圆
C. 平面内的任意一点不在圆上就在圆内
D. 一个圆有且只有一条直径
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市有两个进价不同的书包都卖了60元,其中一个盈利20%,另一个亏本20%,在这笔买卖中,这家超市( )
A. 赚了5元 B. 赔了10元 C. 不赔不赚 D. 亏了5元
相关试题

