Question

【题目】如图，已知抛物线y=﹣x2+mx+3与x轴交于A，B两点，与y轴交于点C，点B的坐标为（3，0）

（1）求m的值及抛物线的顶点坐标．
（2）点P是抛物线对称轴l上的一个动点，当PA+PC的值最小时，求点P的坐标．

Answer 1

【答案】
（1）解：把点B的坐标为（3，0）代入抛物线y=﹣x2+mx+3得：0=﹣32+3m+3，

解得：m=2，

∴y=﹣x2+2x+3=﹣（x﹣1）2+4，

∴顶点坐标为：（1，4）

（2）解：连接BC交抛物线对称轴l于点P，则此时PA+PC的值最小，

设直线BC的解析式为：y=kx+b，

∵点C（0，3），点B（3，0），

∴ ，

解得： ，

∴直线BC的解析式为：y=﹣x+3，

当x=1时，y=﹣1+3=2，

∴当PA+PC的值最小时，点P的坐标为：（1，2）．

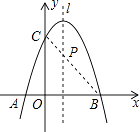
【解析】（1）首先把点B的坐标为（3，0）代入抛物线y=﹣x2+mx+3，利用待定系数法即可求得m的值，继而求得抛物线的顶点坐标；（2）首先连接BC交抛物线对称轴l于点P，则此时PA+PC的值最小，然后利用待定系数法求得直线BC的解析式，继而求得答案．
【考点精析】解答此题的关键在于理解二次函数的性质的相关知识，掌握增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小．