【题目】为了迎接春节,某县准备用灯笼美化滨河路,许采用A、B两种不同造型的灯笼共600个.且A型灯笼的数量比B型灯笼的 ![]() 多15个.
多15个.
(1)求A、B两种灯笼各需多少个?
(2)已知A、B型灯笼的单价分别为40元、30元,则这次美化工程需多少费用?
参考答案:
【答案】
(1)解:设B型灯管需x个,则A型需( ![]() x+15)个.
x+15)个.
根据题意得x+( ![]() x+15)=600,
x+15)=600,
解得:x=351,
则A型灯笼需 ![]() ×351+15=249(个);
×351+15=249(个);
(2)解:249×40+351×30=20490(元).
答:A型灯笼需249个,B型灯笼需351个,这次美化工程需20490元
【解析】(1)根据题意找出相等的关系量,由A、B两种不同造型的灯笼共600个,A型灯笼的数量比B型灯笼的![]() 多15个;列出方程,求出方程的解;(2)根据A、B型灯笼的单价分别为40元、30元,由(1)中的数值列出算式,求出这次美化工程的费用.
多15个;列出方程,求出方程的解;(2)根据A、B型灯笼的单价分别为40元、30元,由(1)中的数值列出算式,求出这次美化工程的费用.
-
科目: 来源: 题型:
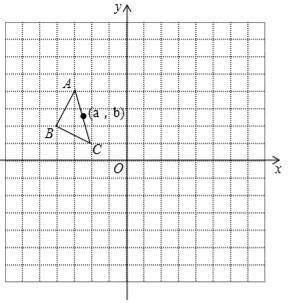
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标为A(﹣3,4),B(﹣4,2),C(﹣2,1),△ABC绕原点逆时针旋转90°,得到△A1B1C1,△A1B1C1向右平移6个单位,再向上平移2个单位得到△A2B2C2.
(1)画出△A1B1Cl和△A2B2C2;
(2)P(a,b)是△ABC的AC边上一点,△ABC经旋转、平移后点P的对应点分别为P1、P2,请写出点P1、P2的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数学兴趣小组活动中,小明进行数学探究活动,将边长为2的正方形ABCD与边长为
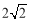 的正方形AEFG按图1位置放置,AD与AE在同一直线上,AB与AG在同一直线上.
的正方形AEFG按图1位置放置,AD与AE在同一直线上,AB与AG在同一直线上.(1)小明发现DG⊥BE,请你帮他说明理由;
(2)如图2,小明将正方形ABCD绕点A逆时针旋转,当点B恰好落在线段DG上时,请你帮他求出此时BE的长;
(3)如图3,小明将正方形ABCD绕点A继续逆时针旋转,线段DG与线段BE将相交,交点为H,写出△GHE与△BHD面积之和的最大值,并简要说明理由.
-
科目: 来源: 题型:
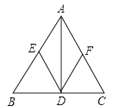
查看答案和解析>>【题目】如图,在△ABC中,AD⊥BC于D,点D,E,F分别是BC,AB,AC的中点.求证:四边形AEDF是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在-2,-1,0,1,2中,不等式x+3>2的解有( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.a5+a5=a10
B.a6×a4=a24
C.a0÷a﹣1=a
D.a4﹣a4=a0 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列关系式中,正确的是( )
A.(a+b)2=a2﹣2ab+b2
B.(a﹣b)2=a2﹣b2
C.(a+b)2=a2+b2
D.(a+b)(a﹣b)=a2﹣b2
相关试题

